2’s Complement Representations

二进制补码数制表示负数

reference： P31

What is 2’s complement?

原数制是通过改变符号将一个数变为负数，而补码数制是通过补码来表示负数。也就是说一个数（10进制）的补码是这个数（10进制）的负数 负数不能直接读，判断一个负数是多大，必须用补码

n位数B的补码为2^n 的二进制数- B的二进制数

7（0111）=> -7(10000-0111)

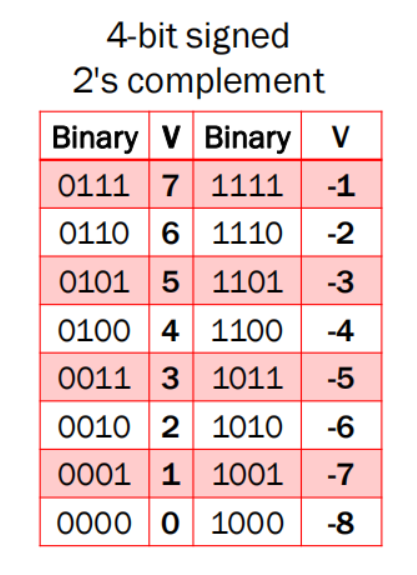
image-20221004095541152

对应码相加为10000（2^3）所以-4的码为 10000-4的后四位码

注意表示范围为（-8，7）$（-2^{n-1},2^{n-1}-1）$

  • Assume N bits are used, for a value –A,

  • 2’s complement representation is defined as 2^N（1后面加N个0） – A

  • the MSB (leftmost) represents the sign(正负号) (bit)

​ 0: positive

​ 1: negative

简便算一个数的补码(负数的码)的方法：Invert all bits and add 1

image-20221103125258341

举例：

image-20221004095609147

Why 2’s Complement?

It eliminates the need of subtraction.

A – B = A + (-B) = A + (2’s complement of B)

把减法转为加法

image-20221003214903990

image-20221003214038713

-7没溢出 ▶ 丢弃最高位！

sign extension（符号扩展）

image-20221003213243981

将4的码扩展一位表示符号（0-> +）取补后得到新的符号扩展位上仍然为对应的符号（1 -> -）

image-20221003213521520

Overflow

Overflow happens when an operation produces a result outside the range that can be represented by N bits – either larger than the maximum or lower than the minimum representable value.

两个异号数相加肯定不会溢出

同号数相加看最高两位carry的值是否异号：异号溢出，同号不溢出（XOR）

image-20221003214736225