缓存替换算法
Cache Replacement Policies - introduction
缓存替代算法读书笔记,记录Cache Replacement Policies的内容
introduction
数据访问的延时远远超过指令执行延时,因而需要缓存。
对于缓存,使用命中率来衡量有效性:定义$s/r$ 其中s是缓存处理的内存请求,r是向缓存发出的总内存请求。
提高缓存命中率有几种方法。一种方法是增加缓存的大小,通常会以增加延迟为代价。第二种方法是增加缓存的关联性,这会增加缓存线可以映射到的可能位置的数量。
在一个极端情况下,直接映射缓存(关联性为1)将每个缓存线映射到缓存中的一个单一位置。在另一个极端情况下,全关联缓存允许缓存线放置在缓存的任何位置。
选择一个好的缓存替换策略是为了避免因关联性过大而导致资源和设计复杂度增加
分类
• Insertion Policy: 当新的行被插入到缓存时,替换策略如何初始化该行的替换状态?
• Promotion Policy: 当某一行在缓存中命中时,替换策略如何更新该行的替换状态?
• Aging Policy: 当有竞争行被插入或Promote时,替换策略如何更新某行的替换状态?
• Eviction Policy:在固定数量的选择中,替换策略会驱逐哪一行?
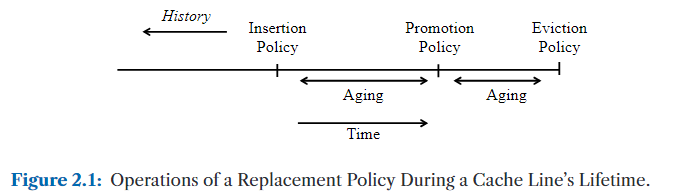
粗粒度策略在插入时对所有缓存行一视同仁,因此它们主要依赖巧妙的Aging和Promote策略来操纵替换优先级。
细粒度策略采用更智能的插入策略。当然,细粒度策略也需要适当的Aging和Promote来更新替换状态,因为在插入时无法预测所有行为。
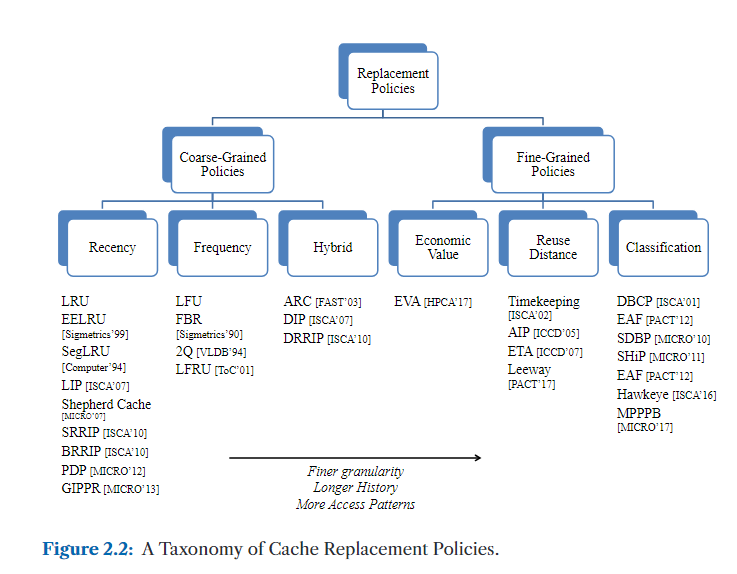
粗粒度策略(Coarse-Grained Policies)
粗粒度策略在缓存行(cache line)首次插入缓存时对所有缓存行一视同仁,它们通过观察缓存行在缓存中的重用行为(reuse behavior)来区分“缓存友好型”(cache-friendly)与“缓存不友好型”(cache-averse)数据。我们进一步根据用于区分缓存驻留行的度量标准,将粗粒度策略划分为三类:
- 第一类(也是粗粒度策略中的主流)是基于访问新近性的策略(Recency-Based Policies),它们按照缓存行最近被访问的时间顺序进行排序。
- 第二类是基于访问频率的策略(Frequency-Based Policies),它们依据缓存行被访问的次数进行排序。
- 第三类是自适应策略(Hybrid Policies),它们动态监控缓存行为,随着时间推移选择当前阶段最合适的粗粒度策略。
基于新近性的策略(Recency-Based Policies)
这类策略根据缓存行在其生命周期中的最新一次访问时间对其排序。为实现这种排序,策略通常维护一个逻辑新近性栈(recency stack),用于表示缓存行被访问的相对顺序。不同策略以不同方式利用该新近性信息。
例如,常用的最近最少使用(LRU)策略及其变种倾向于淘汰最久未被使用的缓存行,而最近最多使用(MRU)策略则倾向于淘汰最近被访问过的缓存行。还有一些策略则采用中间折衷的淘汰方式。
我们进一步将新近性策略根据其观察生命周期的定义进行划分:
- 第一类定义缓存行的生命周期在其被驱逐(evicted)出缓存时终止,称为固定生命周期(fixed lifetime)策略;
- 第二类策略则通过引入一个临时结构(如Victim Cache或Re-Reference Prediction Table),将缓存行的生命周期延长至驱逐之后,使得那些具有较长重用距离的缓存行有“第二次机会”获得命中,我们称这类策略具有扩展生命周期(extended lifetime)。
基于频率的策略(Frequency-Based Policies)
频率策略通过维护访问计数器(frequency counters)来对缓存行进行排序,计数器记录每个缓存行被访问的频率。不同替换策略采用不同方式更新和解释这些计数器:
- 有的策略将计数器单调递增;
- 有的策略则采用“衰老机制”(aging),即随着时间推移逐渐降低计数值;
- 某些策略会直接淘汰计数值最低的缓存行;
- 其他策略则根据预设标准来决定淘汰哪些缓存行。
混合策略(Hybrid Policies)
由于不同的粗粒度策略适用于不同的缓存访问模式,混合策略会在程序执行过程中根据“阶段性行为(phase behavior)”动态地选择最合适的策略。这些策略在“评估周期(evaluation period)”中监测多个候选粗粒度策略的命中率(hit rate),然后根据反馈选择未来访问中最优的策略。
自适应策略的优势在于可以避免单一策略可能出现的性能瓶颈或“路径依赖问题(pathologies)”。
在第3章中我们将看到,先进的混合策略在不同时间段内采用不同的插入优先级(insertion priority)来切换粗粒度策略。尽管插入优先级会随时间变化,这些策略在每个时间段内仍然是粗粒度的,因为在同一时间段内,所有缓存行的处理方式是一致的。
细粒度策略(Fine-Grained Policies)
细粒度策略在缓存行被插入缓存时就对它们进行区分。这种区分依赖于缓存行以往生命周期中的行为信息。例如,如果某条缓存行在过去从未命中过,那么它可以被以低优先级插入缓存。
由于不可能记录所有缓存行的完整历史行为,细粒度策略通常选择对**缓存行的分组(grouping)**进行行为记录。例如,许多策略会将**由同一个加载指令(load instruction)访问过的缓存行**归为一组。
当然,所有细粒度策略的核心问题是:在插入时如何区分这些分组。我们根据所使用的度量方式,将细粒度策略分为两个大类:
- 基于分类的策略(Classification-Based Policies):为每个缓存行分组预测两种可能的状态之一 —— “缓存友好型(cache-friendly)”或“缓存不友好型(cache-averse)”;
- 基于重用距离的策略(Reuse Distance-Based Policies):试图为每个缓存行分组预测更详细的重用距离(reuse distance)信息。
这两类策略分别代表了细粒度策略谱系的两个极端:
- 分类策略只有两个预测值(友好 / 不友好);
- 而重用距离策略则可能预测多个可能值(比如四种、八种等更精细的距离划分);
- 实际上,大多数策略介于两者之间,在多个有限值之间做出选择。
最后,Beckmann 和 Sanchez(2017) 提出了新的预测度量方式,我们将在第三类中对这些新型指标(novel metrics)进行讨论。
基于分类的策略(Classification-Based Policies)
这类策略将即将插入的缓存行划分为两类:
- 缓存友好型(Cache-friendly)
- 缓存不友好型(Cache-averse)
其核心思想是:优先淘汰缓存不友好型的缓存行,以便为缓存友好型行腾出空间。因而,缓存友好型行以更高优先级被插入;在缓存友好型行之间,一般还会根据新近性(recency)维护一个二级排序。
分类策略被广泛认为是当前的先进状态(state-of-the-art)策略,原因如下:
- 它们能够利用缓存行为的长期历史信息做出更智能的决策;
- 它们适用于各种不同的缓存访问模式。
我们将在第 4.2 节详细介绍这类策略。
基于重用距离的策略(Reuse Distance-Based Policies)
这类策略试图为即将插入的缓存行预测其重用距离(reuse distance):
- 如果某条缓存行在超过预测的重用距离之前都未再次被命中,则会被提前淘汰。
这类策略可以看作是“预测版本”的新近性策略或频率策略,因为传统的新近性(如 LRU)或频率策略(如 LFU)其实也是在间接估算重用距离,只不过它们是基于在缓存驻留期内的行为。
而重用距离策略是通过历史信息进行显式预测,因此具备独特的优劣势,我们将在第 4.1 节详细探讨这些内容。
细粒度策略(Fine-Grained Policies)
细粒度策略在缓存行被插入缓存时就对它们进行区分。这种区分依赖于缓存行以往生命周期中的行为信息。例如,如果某条缓存行在过去从未命中过,那么它可以被以低优先级插入缓存。
由于不可能记录所有缓存行的完整历史行为,细粒度策略通常选择对**缓存行的分组(grouping)**进行行为记录。例如,许多策略会将由同一个加载指令(load instruction)访问过的缓存行**归为一组。
当然,所有细粒度策略的核心问题是:在插入时如何区分这些分组。我们根据所使用的度量方式,将细粒度策略分为两个大类:
- 基于分类的策略(Classification-Based Policies):为每个缓存行分组预测两种可能的状态之一 —— “缓存友好型(cache-friendly)”或“缓存不友好型(cache-averse)”;
- 基于重用距离的策略(Reuse Distance-Based Policies):试图为每个缓存行分组预测更详细的重用距离(reuse distance)信息。
这两类策略分别代表了细粒度策略谱系的两个极端:
- 分类策略只有两个预测值(友好 / 不友好);
- 而重用距离策略则可能预测多个可能值(比如四种、八种等更精细的距离划分);
- 实际上,大多数策略介于两者之间,在多个有限值之间做出选择。
最后,Beckmann 和 Sanchez(2017) 提出了新的预测度量方式,我们将在第三类中对这些新型指标(novel metrics)进行讨论。
基于分类的策略(Classification-Based Policies)
这类策略将即将插入的缓存行划分为两类:
- 缓存友好型(Cache-friendly)
- 缓存不友好型(Cache-averse)
其核心思想是:优先淘汰缓存不友好型的缓存行,以便为缓存友好型行腾出空间。因而,缓存友好型行以更高优先级被插入;在缓存友好型行之间,一般还会根据新近性(recency)维护一个二级排序。
分类策略被广泛认为是当前的先进状态(state-of-the-art)策略,原因如下:
- 它们能够利用缓存行为的长期历史信息做出更智能的决策;
- 它们适用于各种不同的缓存访问模式。
我们将在第 4.2 节详细介绍这类策略。
基于重用距离的策略(Reuse Distance-Based Policies)
这类策略试图为即将插入的缓存行预测其重用距离(reuse distance):
- 如果某条缓存行在超过预测的重用距离之前都未再次被命中,则会被提前淘汰。
这类策略可以看作是“预测版本”的新近性策略或频率策略,因为传统的新近性(如 LRU)或频率策略(如 LFU)其实也是在间接估算重用距离,只不过它们是基于在缓存驻留期内的行为。
而重用距离策略是通过历史信息进行显式预测,因此具备独特的优劣势,我们将在第 4.1 节详细探讨这些内容。
设计考虑因素
●粒度:在插入时以何种粒度区分线路?所有缓存线路是否被同等对待,还是根据历史信息赋予不同的优先级?
●历史:替换策略在做出决策时利用了多少历史信息?
● 访问模式:替换策略对特定访问模式的专门化程度如何?它对访问模式的变化或不同访问模式的混合是否具有鲁棒性?
Coarse-Grained Replacement Policies
RECENCY-BASED POLICIES
LRU
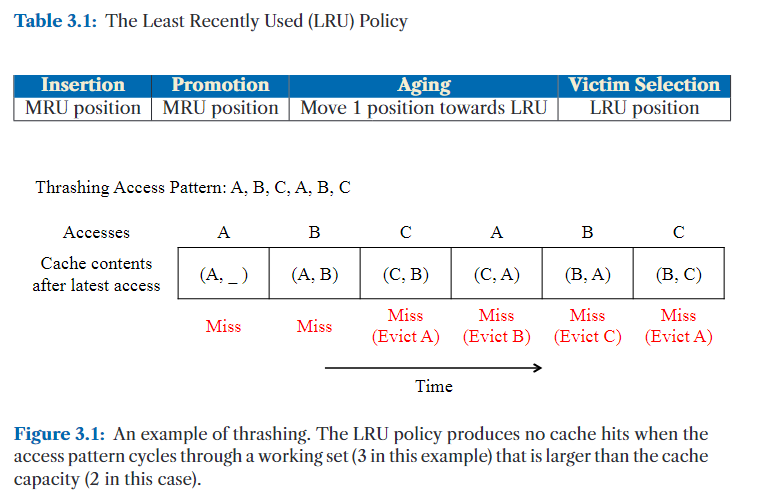
基于最近使用的策略根据最近使用信息对行进行优先级排序。Least Recently Used(LRU)策略由Mattson等人于1970年提出,是最简单和最广泛使用的。
Evice 最老的cache line, 为了找到最老的一行,LRU策略在概念上维护一个最近使用栈,其中栈顶代表最近使用(MRU)的行,栈底代表最少最近使用(LRU)的行。
优势场景
当程序存在时间局部性时候,LRU表现优越。
劣势场景
当应用程序的工作集大小(working set size)超过缓存容量时,LRU 可能变得极为低效,导致一种被称为抖动(thrashing)的现象(Denning, 1968)(见图 3.1)。在这种情况下,缓存不断替换,但始终无法保留即将被重用的数据。
在存在扫描(scan,例如对数组、链表或文件逐项顺序访问。)操作的情况下,LRU 的效果也不佳。它倾向于缓存最近访问过的扫描数据,而这些数据往往不会再次被使用,从而挤掉那些更有可能被重用的旧缓存行。
LRU的变体1 - 最近最常用(MRU,Most Recently Used)策略
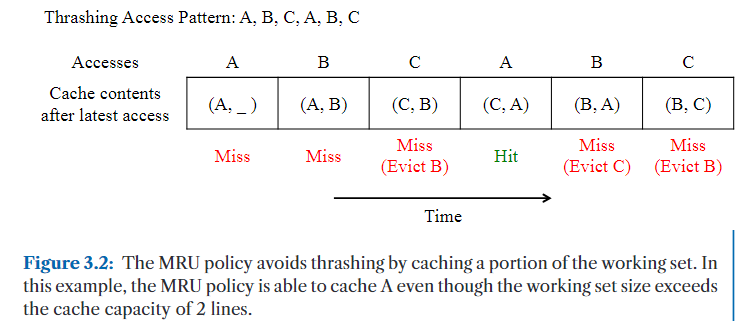
MRU 策略通过优先淘汰最新加载的缓存行,以保留旧的缓存行,从而缓解抖动(thrashing)问题。
因此,当工作集大小超过缓存容量时,MRU 能够保留工作集的一部分,避免频繁全部替换。例如,在图 3.1 中展示的抖动访问模式下,图 3.2 显示 MRU 通过保留部分工作集(在该例中始终不淘汰缓存行 A),提高了相比 LRU 的命中率。

LRU的变体2 - 早期驱逐 LRU(EELRU,Early Eviction LRU)
ELRU 策略通过主动早期驱逐部分缓存行来避免抖动(thrashing)(Smaragdakis 等人,1999)。其核心思想是在检测到工作集大小超过缓存容量时,提前淘汰一小部分缓存行,从而让剩余的缓存行能更有效地通过 LRU 管理。
更具体地说:
- 当工作集能够装入缓存时,EELRU 行为与 LRU 相同,淘汰最久未使用(LRU)的位置的缓存行;
- 当检测到访问模式呈现循环且访问范围超过缓存容量时,它将淘汰第 e 个最近使用(eth most recently used)的位置上的缓存行,即:不是最旧的,而是“中间位置”的缓存行。
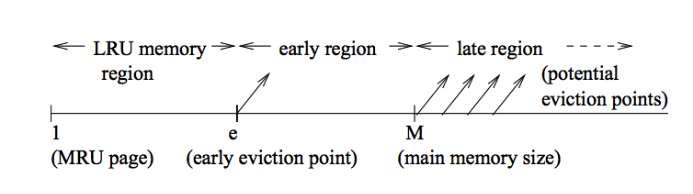
最近性轴(recency axis)分为三个区域:
- 左端(MRU):最近刚被使用的缓存行;
- 右端(LRU):最久未使用的缓存行;
- 位置 e 与 M 之间:中间区域,被分为早期驱逐区(early eviction region)与晚期驱逐区(late eviction region);
EELRU 策略会根据命中位置统计来判断是否采用早期驱逐:
- 如果命中次数从 MRU 到 LRU 单调递减,说明没有抖动,继续用正常的 LRU 策略;
- 如果命中在 LRU 区域多于 early eviction 区域,则说明某些“中间位置”的缓存行不值得保留,于是从 eth 位置驱逐,保留 LRU 区域的“老”缓存行。

LRU的变体3 - 分段 LRU(Segmented LRU,Seg-LRU)
Seg-LRU 策略专门为“扫描型访问(scanning accesses)”设计优化,通过优先保留那些至少被访问过两次的缓存行,有效避免将一次性访问的数据占满缓存空间(Karedla 等,1994)。
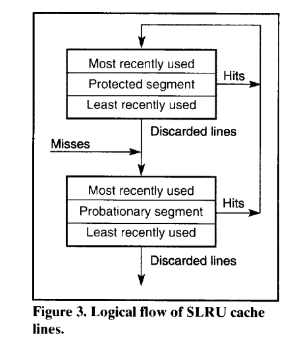
Seg-LRU 将传统的 LRU 栈逻辑上划分为两个区域(见图 3.4):
- 试用段(Probationary Segment):
- 新加入缓存的行被插入到该段;
- 如果这些行未被再次访问,将被淘汰;
- 保护段(Protected Segment):
- 当某条缓存行在试用段中命中一次后,会被提升到保护段;
- 表示这条数据被访问过至少两次,因而被认为是“有价值的”。
淘汰逻辑:
- 淘汰操作仅从试用段中选择最久未使用(LRU)的位置;
- 扫描型访问的数据因只被访问一次,永远不会被提升到保护段,因此很快被淘汰,不会污染缓存;
- 被提升到保护段的缓存行如果空间不足,会将保护段的 LRU 行“降级”回试用段的 MRU 位置,给予其“第二次机会”;
- 这样旧数据最终会慢慢滑出保护段,适应工作集变化。

LRU的超越1 - LRU 插入策略(LIP,LRU Insertion Policy)
即将新加入的缓存行插入到 LRU 位置(最久未使用)而不是通常的 MRU 位置(最近使用);
如此一来,新插入的行很快就会被淘汰,模拟了 MRU 的行为(MRU 策略是优先淘汰最新加入的数据);

这个发现启发了许多新型替换策略的设计,它们专注于:
- 修改插入策略(Insertion Policy)
- 修改提升策略(Promotion Policy)
LRU的超越2 - 双模插入策略(BIP, Bimodal Insertion Policy)
传统的抗抖动(thrash-resistant)策略如 LIP(LRU 插入策略)和 MRU,虽然对固定的工作集效果较好,但当工作集发生阶段性变化(phase change)时,它们无法很好地适应。
BIP 通过引入概率性插入机制对这一问题进行了改进:
- 主要插入位置:LRU 位置(像 LIP 一样,具备抗抖动能力)
- 但以小概率 ε 插入到 MRU 位置(可保留近期数据,应对工作集变化)
- 常用 ε 值:概率1/32 或 1/64
- ε = 0 等同于 LIP(全部插入到 LRU)
- ε = 1 等同于 LRU(全部插入到 MRU)

LRU的超越3 - 静态再引用间隔预测策略(SRRIP, Static Re-Reference Interval Prediction Policy)
Jaleel 等人在研究中提出,将缓存替换问题看作再引用间隔预测(RRIP)问题。而传统的 LRU(最近最少使用)链条,其实也可以视作一个RRIP 链条。具体而言:
- 在 LRU 链条 中,一个缓存行的位置代表自上次使用以来的时间间隔。
- 在 RRIP 链条 中,缓存行的位置则代表预计它下次被引用的时间间隔。
RRIP 使用一个 2 位 RRPV(Re-reference Prediction Value)值 来表示缓存行的预期引用间隔:
- 00 = 预计最先被重用(即最短的再引用间隔)
- 11 = 预计最晚被重用(即最长的再引用间隔)
SRRIP 的操作机制
SRRIP 提出了一个折中的解决方案,通过设置中等的 RRPV 值来兼顾不同的访问模式,并通过对缓存行的升迁和驱逐来防止扫描模式(即一次性大量访问不重用的数据)对缓存的破坏。与 LRU 和其他策略不同,SRRIP 使得可以同时适应时间局部性访问和扫描访问。

LRU的超越4 - 双模再引用间隔预测策略(BRRIP)
上两种的结合
BRRIP 是 SRRIP 的一种扩展,目的是在缓存策略中加入对扫描抗性(scan-resistance)的增强,并提供对抖动模式(thrashing)更强的抵抗力。通过与 BIP(双模插入策略)的结合,BRRIP 使得缓存策略在混合模式下表现得更加灵活。
BRRIP 的基本操作
BRRIP 的关键思想是,在大多数缓存行插入时使用 RRPV = 3(即预计该缓存行在未来很久后才会被重用),而偶尔会以 概率 ε 插入 RRPV = 2 的缓存行,这样能够适应不同的访问模式。
RRIP主要解决抖动问题,而动态主要解决扫描问题
LRU的超越5 - 保护距离基础策略(PDP)
PDP(保护距离基础策略)是Duong等人在2012年提出的动态缓存替换策略。它是RRIP策略的改进版,通过动态估算保护距离(PD)来保护缓存行免于被替换。PD是一个度量值,表示缓存行在被驱逐之前,需要经过多少次访问。
PDP的关键概念:
- 保护距离(PD):
- PD是表示缓存行重用频率的一个值。它是动态计算的,并反映了程序的访问模式。
- 它是通过重用距离分布(RDD)计算得出的,RDD表示在程序执行的某个时间段内观察到的重用距离的分布。
- PD的选择是为了覆盖缓存中大多数缓存行的访问模式,即大多数行的重用距离小于或等于PD。
- 重用距离分布(RDD):
- RDD是缓存行在每次重用之间的访问次数的分布。PD被设置为能够覆盖大多数重用距离。
- 例如,对于应用程序436.cactusADM,RDD可能表明大多数缓存行的访问发生在64次以内,因此PD将设置为64。
- PD的重新计算是一个不频繁的过程,以适应应用程序访问模式的变化。
- 剩余保护距离(RPD):
- 当缓存行被插入或提升时,会为其分配一个剩余保护距离(RPD),其初始值为当前的PD。
- 每当访问一个集合时,集合中每个行的RPD值会减少1,从而使该行逐渐变得不再受保护。如果RPD为0,则该行不再受保护,可以被替换。
- 只有当RPD为0时,缓存行才可以被驱逐,这确保了那些经常被重用的行不容易被替换。
LRU的超越5 - 遗传插入与提升策略(GIPPR)
GIPPR(Genetic Insertion and Promotion for PseudoLRU Replacement)是一种基于RRIP的缓存替换策略,由Jiménez等人在2013年提出。GIPPR通过引入插入/提升向量(IPV),将插入和提升策略进行了推广。IPV为缓存行在插入和提升过程中指定新的位置。
IPV的概念:
- IPV指定了一个缓存行的新位置,无论是在插入时还是在从其他位置提升时。在一个k路组相联缓存中,IPV是一个k + 1长度的整数向量,范围从0到k-1,其中第i个位置的值表示当第i个位置的缓存行被重新引用时,它应被提升到的新位置。
- IPV的第k个位置表示新插入的缓存行应该插入的位置。
- 如果新位置小于旧位置,则缓存行会被向下移动以腾出空间;
- 如果新位置大于旧位置,则缓存行会被向上移动以腾出空间。
IPV的使用:
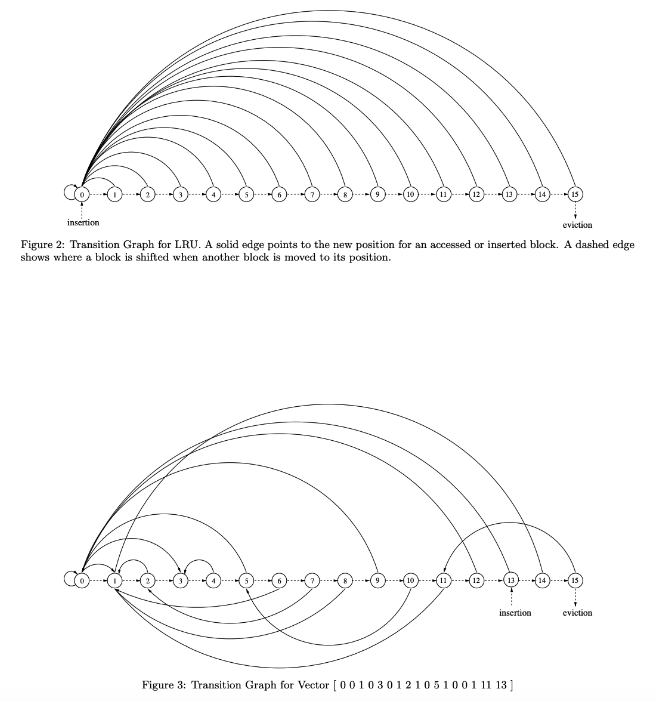
- LRU策略的IPV通常是一个简单的向量(如图3.7的顶部部分所示),其中每个缓存行的插入和提升位置按照LRU顺序进行。
- 然而,通过遗传算法演化出的IPV(图3.7底部部分所示)则可能是一种更复杂的插入和提升策略,旨在根据特定的工作负载优化缓存行的管理。
遗传算法和IPV的演化:
- Jiménez等人通过使用离线遗传搜索方法,针对SPEC 2006基准测试中的不同工作负载,进化出了良好的IPV。遗传算法通过不断地优化IPV,使其能够适应不同的缓存访问模式。
- 遗传算法的搜索过程能够探索大量可能的IPV(对于一个k路缓存,可能的IPV数量为$k^{k+1}$,因此它能够找到最适合特定工作负载的插入和提升策略。
工作负载适应性:
- 由于没有一个通用的插入策略或RRIP策略能够适应所有的工作负载,最佳的IPV也会因工作负载而异。
- 因此,Jiménez等人提出了一种混合解决方案,即使用集合对抗(set dueling,见第3.3节)来同时考虑多个IPV,从而实现最优的性能。
图示:
图3.7展示了两种示例IPV:第一种是表示LRU策略的简单IPV(上图),第二种是通过遗传算法演化出来的更复杂的IPV(下图),该IPV在插入和提升策略上提供了更高的灵活性和优化空间。
扩展生命周期的基于近期的策略
扩展生命周期策略(Extended Lifetime Policies)是近期基于策略的一个特殊类,通过将一些缓存行存储在辅助缓冲区或受害缓存中,人工延长它们的生命周期。这样做的关键动机是将缓存替换决策推迟到稍后时机,届时可以做出更有信息支持的决策。这种策略允许粗粒度的缓存替换策略稍微扩展缓存命中的重用窗口,使其大于缓存的大小。
Shepherd Cache(牧羊缓存)
Shepherd Cache模仿了Belady的最优替换策略。由于Belady的策略需要知道未来的访问模式,Rajan等人通过辅助缓存(称为Shepherd Cache)模拟了这种未来的预见性。具体而言,缓存被逻辑上分为两个组件:
- **Main Cache (MC,主缓存)**:该组件模拟最优替换。
- Shepherd Cache (SC,牧羊缓存):该组件使用简单的FIFO替换策略。
Shepherd Cache通过提供一个预见窗口来支持主缓存中的最优替换。新的缓存行最初存储在SC中,替换主缓存中的候选项的决策被推迟,直到新缓存行从SC中被淘汰。与此同时,SC中存储的信息帮助了解主缓存中候选行的重用顺序。例如,那些较早被重用的缓存行变得不太可能被替换,因为Belady的策略会淘汰那些最远将在未来被重用的缓存行。当新行从SC中被逐出时,替换候选项是从MC中挑选出那些在预见窗口内没有被重用的行,或者选择最近被重用的行。如果在新行被SC逐出时,MC中的所有行都已在该行被重用之前被重用了,那么该SC行会替换掉自身。
尽管SC和MC在逻辑上是分开的,Rajan等人通过组织缓存结构,使这两个逻辑组件能够作为单一的物理结构来工作,从而避免了数据在两个组件之间的移动。
Shepherd Cache的作用是通过帮助延长缓存行在MC中的生命周期,从而模拟更优的替换策略。使用Shepherd Cache的权衡是:当预见窗口较大时,MC中的替换接近于最优,但较大的预见窗口会导致主缓存的容量减少。
Shepherd Cache的局限性:
然而,后来的工作(Jain和Lin [2016])表明,要接近Belady的MIN策略的行为,该策略需要的预见窗口大小是缓存大小的8倍,这意味着需要显著增加预见的开销。
FREQUENCY-BASED POLICIES
与依赖“最近使用”不同,基于频率的策略(Frequency-Based policies)利用访问频率来识别被替换的缓存行,因此访问更频繁的行相对于访问较少的行更倾向于保留在缓存中。这种方法不太容易受到扫描操作(scans)的干扰,并且相比仅考虑上一次使用,它具有在更长时间范围内反映重用行为的优势。
最少使用频率(LFU, Least Frequently Used)策略
最简单的基于频率的策略是最少使用频率(LFU, Least Frequently Used)策略(Coffman 和 Denning 于 1973 年提出)。该策略为每个缓存行关联一个频率计数器。当缓存行被插入时,频率计数器初始化为 0,每次访问该行时,计数器加一。在发生缓存未命中(miss)时,淘汰频率最低的候选项。表 3.9 总结了该策略的操作:
然而,基于频率的策略在适应应用程序阶段性变化方面表现不佳,因为来自先前阶段的高频缓存行即使在当前阶段不再被访问,也仍然留在缓存中。

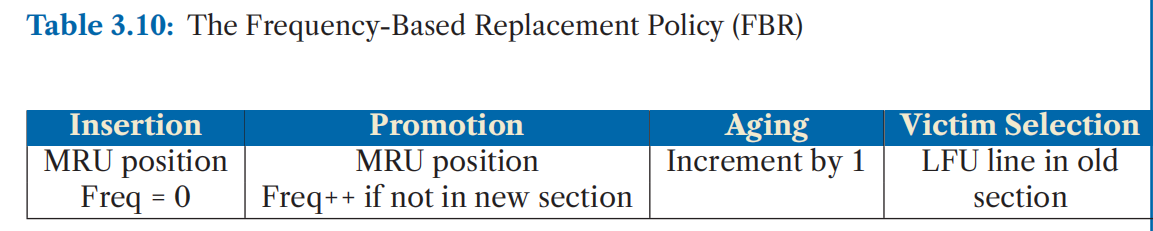
频率替换策略(FBR,Frequency-Based Replacement)
频率替换策略(FBR,Frequency-Based Replacement)**由 Robinson 和 Devarakonda [1990] 提出。他们指出,基于频率的方法容易受到**短暂时间局部性突发访问**的误导,使得频率计数出现虚高。因此,FBR 通过有选择地增加频率计数器的方式,将局部性影响从频率统计中剔除**。
具体来说,FBR 不会对 LRU 栈顶的部分(称为“新区域”)中的缓存行增加频率计数器。这样,短暂的时间局部性(即数据在短时间内被频繁访问)不会影响频率的统计。如图 3.8 所示,这种策略避免了错误提升缓存行的重要性。
然而,该策略存在一个缺点:一旦缓存行从新区域“老化”出去,即便是经常被访问的行,也会因为频率计数增长不够快而被迅速淘汰。
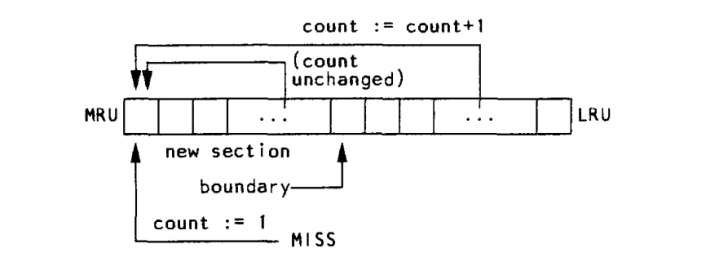
为了解决这个问题,FBR 进一步将替换操作限制在“旧区域”**中——即 LRU 栈底部那些**很久未被访问**的缓存行。中间部分则称为“中间区域”,用于让频繁访问的缓存行有足够时间积累频率值**。
表 3.10 总结了 FBR 策略的操作方式:
LRFU(最近最不频繁使用)策略
背景与动机:
- LRU(最近最少使用)和 LFU(最少使用)是缓存替换策略的两个极端。
- LRFU 是一种融合两者优点的策略,在「时间局部性」和「访问频率」之间实现灵活权衡。
核心思想:
- 引入新度量:CRF(Combined Recency and Frequency)
- 表示某个缓存块的综合访问价值。
- 由该块所有历史访问的“贡献值”累加而成。
- 贡献值的权重由函数 F(x) 决定
- 其中 x 是过去某次访问距当前时间的距离。
- F(x) 是一个随时间衰减的函数 → 越久远的访问贡献越低。
- 策略调节能力:
- 若 F(x) 对所有访问一视同仁 ⇒ 模拟 LFU。
- 若 F(x) 只重视最近一次访问 ⇒ 模拟 LRU。
- LRFU 是一种可调节的缓存替换策略,通过 “加权访问历史” 来同时考虑“访问次数”和“最近访问时间”。
- 当你希望更看重“频率”时,就给每次访问相等的权重;
- 当你希望更看重“最近访问”时,就让权重随时间指数衰减。
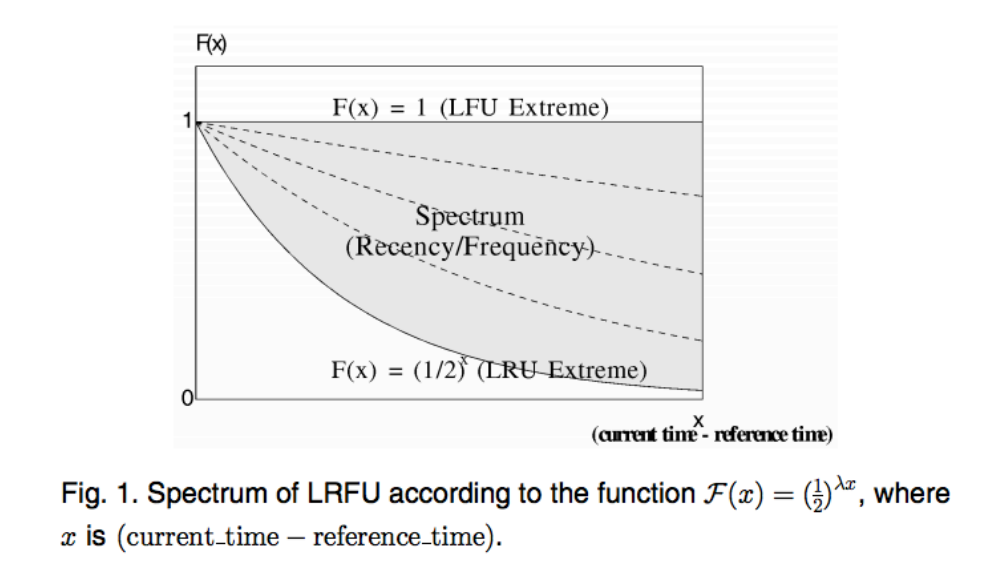
LRFU 在公式 3.1 中使用了一个权重函数,其中 λ 是通过经验选择的参数。
这个权重函数会对较早被访问的数据块赋予指数级更低的优先级,
从而使得 LRFU 能够保留基于频率替换策略的优点,同时实现对旧数据块的平滑老化(即逐渐淘汰)。


LRFU 的性能在很大程度上依赖于参数 λ,因此后续提出的 ALRFU 策略会动态调整 λ 的取值(Lee 等人,1999年)。



