电信系统-1-First half
first half
Telecoms Systems
introduction
repeater作用
When a signal travels through a channel, it suffers attenuation, distortion and noise contamination. Since their negative effects increase with the distance, special equipment called repeaters are inserted along the way.
由于存在损耗,在线路上传输的信号功率会逐渐衰减,衰减到一定程度时将造成信号失真,因此会导致接收错误。中继器就是为解决这一问题而设计的。它完成物理线路的连接,对衰减的信号进行放大,保持与原数据相同。
在模拟系统中,传输的是连续变化(continuously- varying)的波形。为了保持发射波形,中继器主要对信号进⾏滤波、均衡和放⼤。(filter, equalize and amplify the signal)
analog systems: repeaters essentially filter, equalize and amplify the signal.
In digital systems sequences predefined waveforms (symbols) are transmitted. In this case, repeaters regenerate such waveforms
Transmission impairment
媒介中信号传输会有 impairment(损失)其中包括:
attenuation 衰减, distortion 失真 and noise 噪声.
如何去让信号的传输更加稳定可靠,就是本课程的目的。我们关注信号的处理方式,以及信道的设计等等,以尽可能的减少Impairment,让通信过程更加可靠。
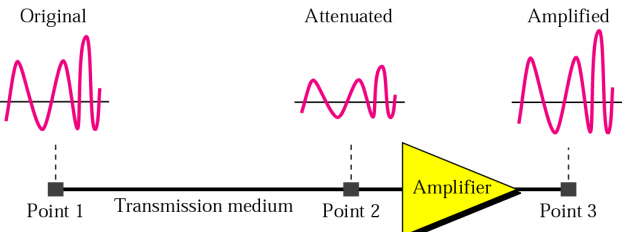
Attenuation
loss of energy for overcoming the **resistance **of medium(克服介质的阻⼒).
amplifiers(放大器) are used to boost the signal back up to its original level(compensate for energy loss)
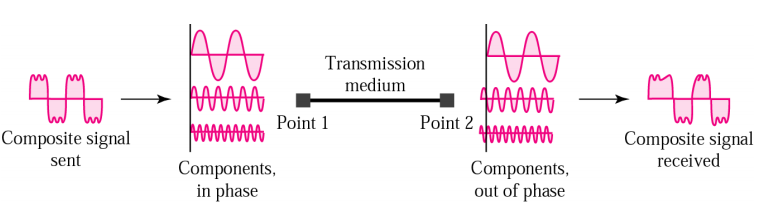
Distortion
signal changes in its form or shape.
Typically effects complex or composite signals: the composite signal carrying different frequencies suffers from the delay of some of these frequencies (第二行和第三行delay了)
通常影响复杂信号(complex)或者合成信号(composite signal)
Each frequency component has its own propagation attenuation through a medium.
Noise
◆ Noise is the main source of a signal being corrupted
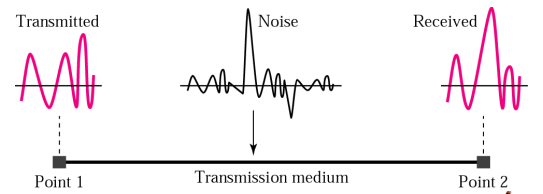
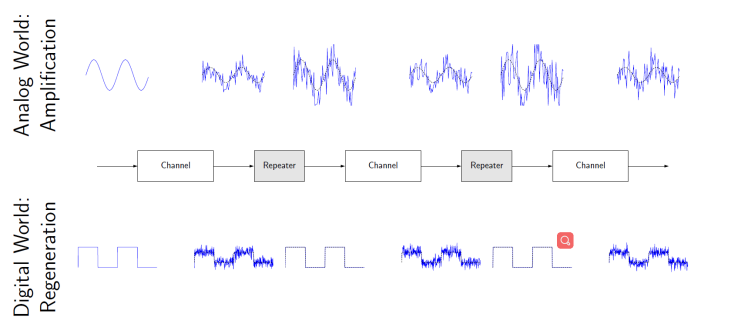
可以看出analog信号在传输过程中比digital更容易失真
WIRELESS COMMUNICATIONS
Types of wireless network
◆ WPAN (Wireless Personal Area Network)
– typically operates within about 30 feet
无线个人网:主要用于个人用户工作空间,典型距离覆盖几米,可以与计算机同步传输文件,访问本地外围设备,如打印机等。目前主要技术包括蓝牙(Bluetooth)和红外(IrDA)。
◆ WLAN (Wireless Local Area Network)
– operates within 300 yards
无线局域网:主要用于宽带家庭、大楼内部以及园区内部,典型距离覆盖几十米至上百米。目前主要技术为802.11系列。
◆ WMAN (Wireless Metropolitan Area Network )
– operates within tens of miles
◆ WWAN (Wireless Wide Area Network )
– operates over a large geographical area, mobile phone,
无线城域网和广域网:覆盖城域和广域环境,主要用于Internet/email访问,但提供的带宽比无线局域网技术要低很多。
Why wireless?
◆ No more cables
◆ Mobility and convenience
◆ Flexibility
◆ Scalability
INFORMATION CONVERSION
Formatting Data

Different sources of information need different methods to transform the source information to a digital format( minimise bitrate but maintain quality)
– Text – ASCII (used to be others)
Each alphanumeric character is transformed into binary by character coding. Most popular character coding method is ASCII
– Voice (PSTN) – Pulse Code Modulation (G711a/u) 64kps
– Voice (GSM) – GSM codec (13kbps) EFR (improved quality)
– 3G WCDMA – AMR (adaptive Multi Rate)
– Picture – JPEG …..
– Video – MPEG2, MPEG4, H264
可靠的通信系统传输信息
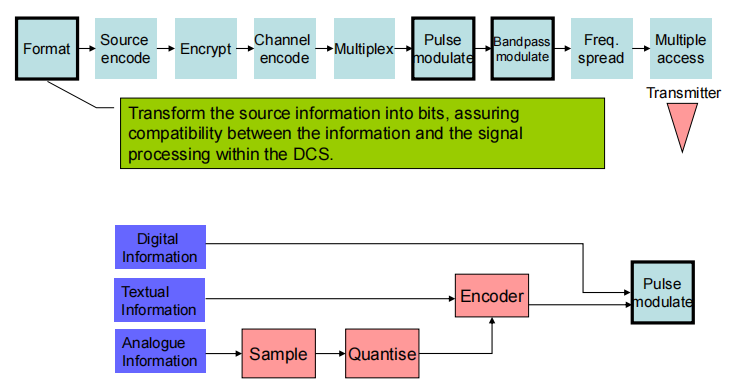
pulse shaping : 脉冲整形是改变传输脉冲波形的过程。其目的是使发射的信号更适合其目的或通信信道,通常是通过限制传输的有效带宽。
Multiplex: 传输媒体的带宽或容量往往会大于传输单一信号的需求,为了有效地利用通信线路,希望一个信道同时传输多路信号,这就是所谓的多路复用技术(Multiplexing)。
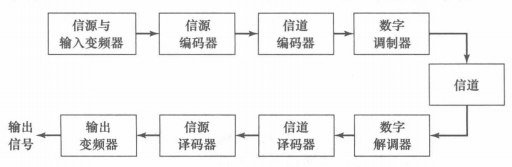
信源输出可以为 模拟 OR 数字;信源编码器把analog or digital signal转成二进制符号表示(被称为信息序列);信道编码器以受控的方式向信息序列中提供某种冗余,以克服噪声和信道干扰对信道造成的失真;数字调制器把二进制序列映射成信号波形,是与信道的接口。
数字解调器把传输波形映射为信号编码,判断波形是0/1,
模数转换
数字信号的传输抗干扰能力更强,且可引入加密技术。所以为了使用数字信号,必须把模拟信号转换:
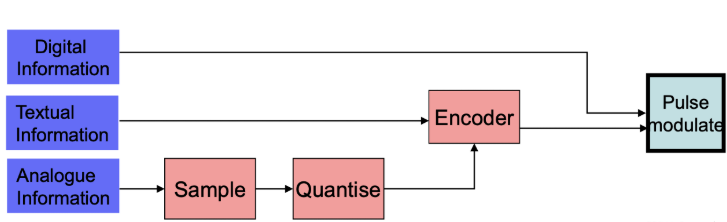
将模拟信号转换为数字信号需要三个步骤,统称为调制:
采样(sampling):对模拟信号抽样得到时间离散幅值连续的信号
量化:对有可能有无穷多个取值的抽样值进行近似,将其表现为有限个数值
编码:把0/1比特序列分配到量化器的不同输出
将模拟信号转化为数字信号的过程就叫做数字化。因此,数字化包括将模拟信息在时间上和幅度上都要离散化,时间上离散化是采样 sampling,幅度上离散化是量化 quantisation

SAMPLING
Analog information has the following properties:
• Continuous in time.
• Continuous in amplitude.
digital information is:
• Discrete in time.
• Discrete in amplitude.
digitization on**(数字化) consists of discretising analog information both in time (sampling) and in amplitude (**quantisation)
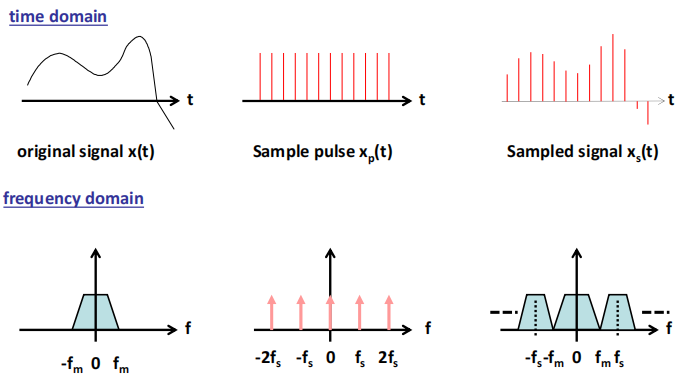
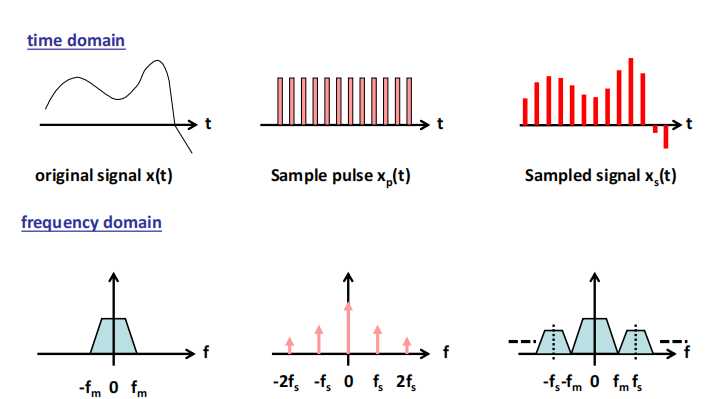
时域和频域的对应关系:
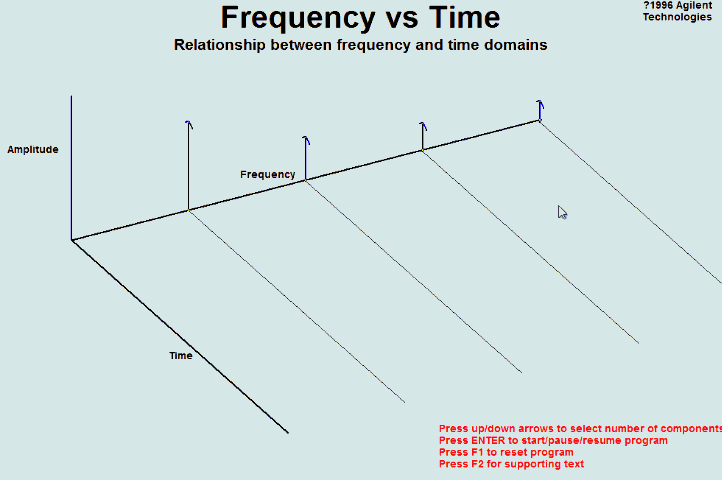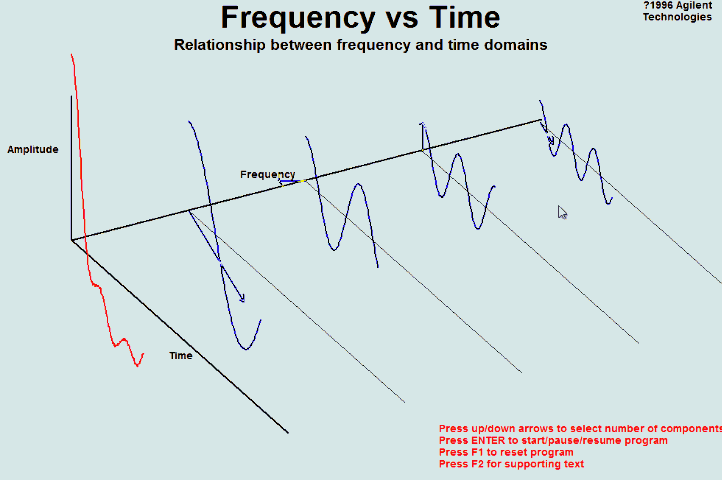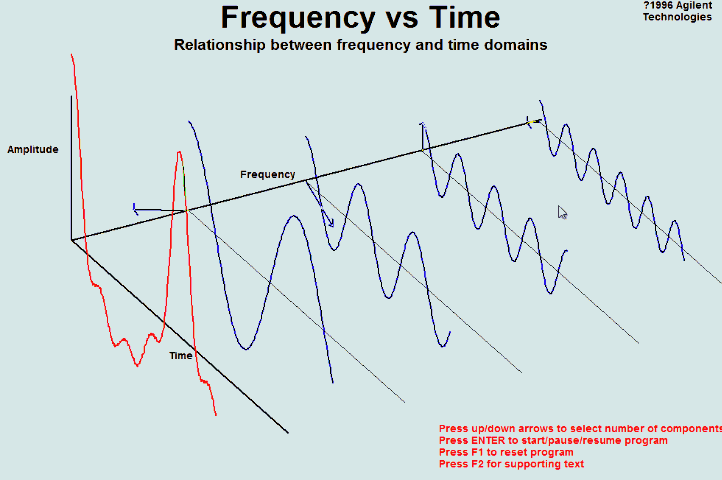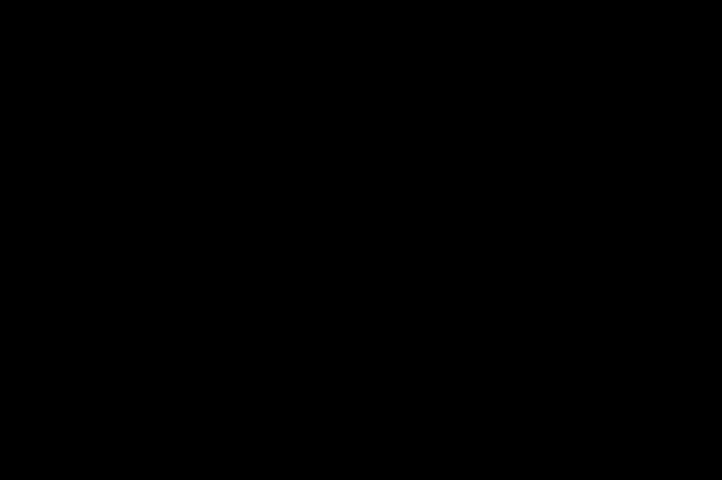
Sampling in the Time Domain
乘 a train of impulses
The quantity Ts is known as the sampling period and fs = 1/Ts is the sampling frequency
Sampling in the Frequency Domain
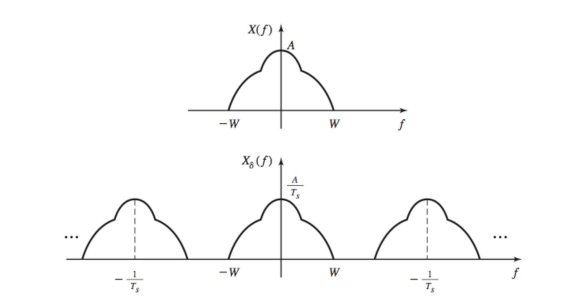
By using the convolution property, we can prove that the spectrum of a sampled signal consists of replicas of the original spectrum centred at multiples of the sampling frequency
频域表现为象以采样频率搬移
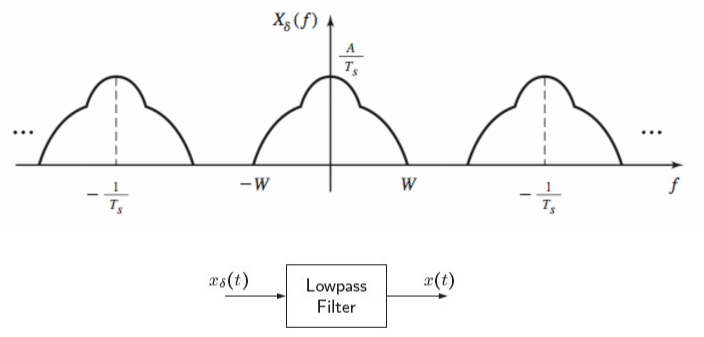
Interpolating for D/A conversion
可以还原采样前信号
最理想条件下的采样:
单位冲激:
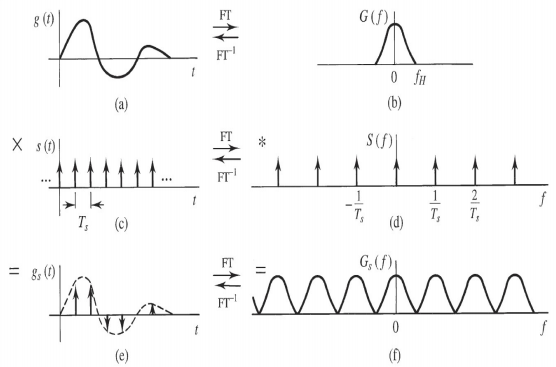
(a) signal g(t); (b) signal spectrum; (c) sampling function;
(d) spectrum of sampling function; (e) sampled signal;
(f) spectrum of sampled signal
方波:
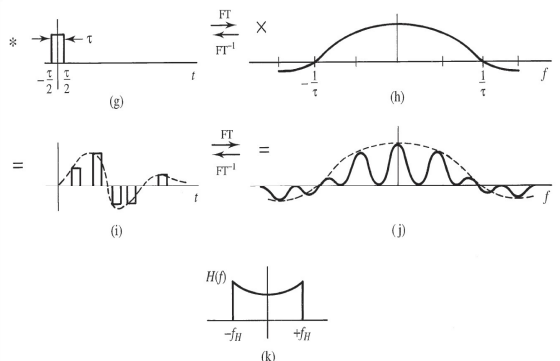
(g) finite width sample; (h) spectrum of (g); (i) sampled signal;
(j) spectrum of (i); (k) receiver equalizing filter to recover g(t)
Sampling Theorem (Nyquist’s Criterion)
To prevent aliasing and hence to allow the original signal to be recovered the sampling frequency (fs ) must be given by:
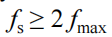
where fmax is the highest frequency present in the original signal.
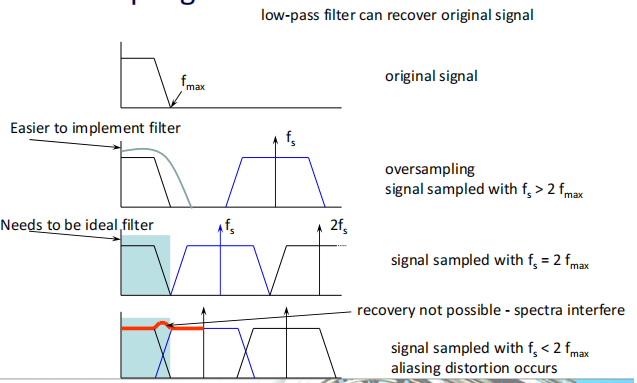
Oversampling makes it easier to design a simpler filter to recover the original signal
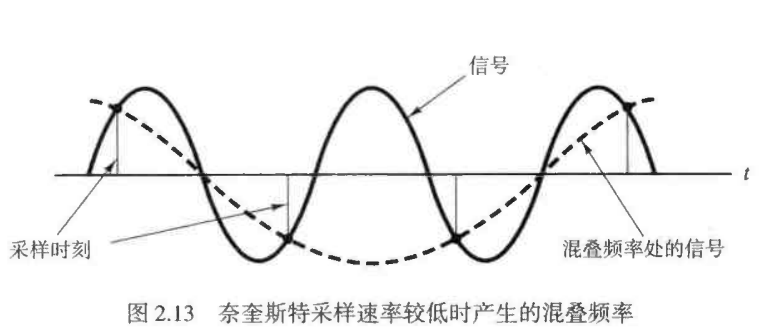
混叠在时域中的表现:由于结果的不定性,根据欠采样点可能会画出一条完全不同的正弦曲线
QUANTISATION
抽样使时间离散,但是幅度仍然连续。必须通过量化使幅度值也离散,才可以得到数字信号
困惑:为啥说幅度值是连续的?
这里是针对于非理想(自然)采样结果来说,采样后的结果中,每个自然采样的幅度仍然有无穷多种可能的取值,而数字系统只能处理数量有限的数据
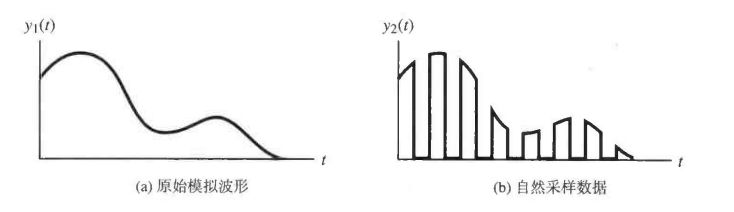
量化的目的是为了让脉冲的幅度值离散,且限制在一个有限集合中
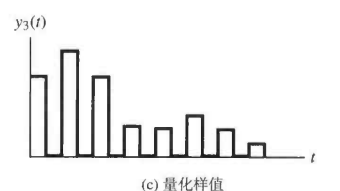
Results from mapping continuous analogue values to discrete values that can be represented digitally
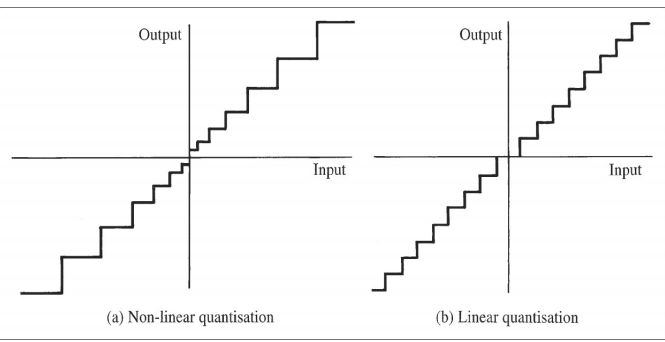
May be uniform or nonuniform
Pulse-code modulation (PCM) is a method used to digitally represent sampled analogue signals
量化原理
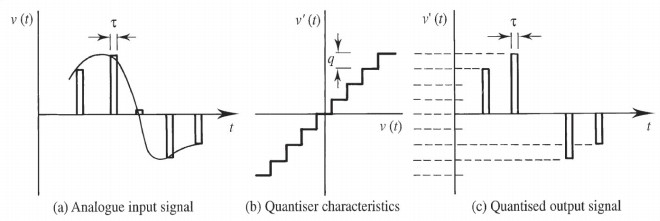

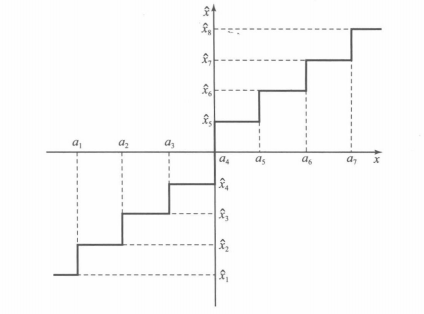
对于赋值来说,设置不相交的量化区间(Quantisation Region)如果幅度值在某个量化区间内,则把该幅度值近似赋为该量化区间对应的量化电平(Quantized value),再将这些电平按二进制编码(假设有N种可能电平) 个比特就足够表示这N个电平。但是在这个过程中会引发Quantisation distortion
个比特就足够表示这N个电平。但是在这个过程中会引发Quantisation distortion
均匀量化uniform Quantisation
Quantisation interval, q,(step size)(区间长度) uniformly distributed over the full range(量化区间均匀分布)
The approximation will result in an error no larger than ±q/2
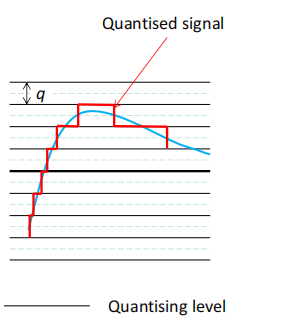
Quantising distortion
量化失真
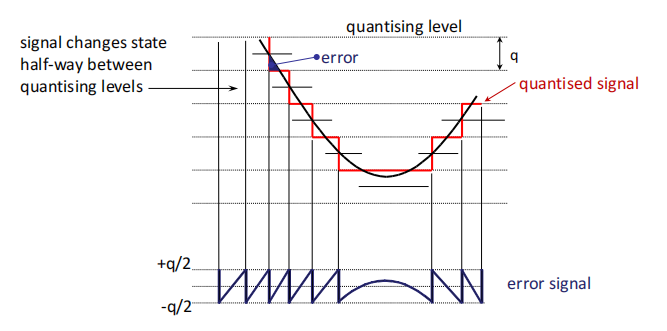
量化函数的差值一直在-q/2和q/2之间来回变,上面和下面那个error signal是一直对应的。幅度横跨整个数字位宽表示范围的信号,其四舍五入的量化误差可以通过一个峰峰值幅度为q的锯齿波形来表示。
Error (e) is approximately sawtooth over the quantization region, apart from the dwell regions.
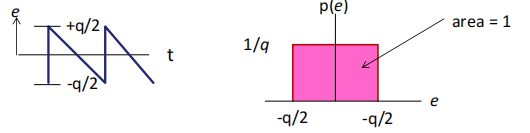
A sawtooth waveform has a uniform pdf: all values are equally likely. The area under the pdf must be 1 so that the amplitude is 1/q. Note that p(e)=0 outside the range +q/2 to -q/2
the power of the quantization error is 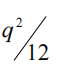
distortion power is constant and depends only on the step size.
SQNR
SQNR (Signal to Quantisation Noise Ratio 信号量化噪声比 简称量噪比)来衡量量化后的性能
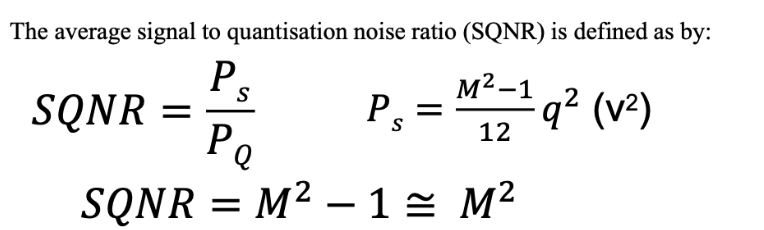
其中M是Number of quantisation level(电平数)
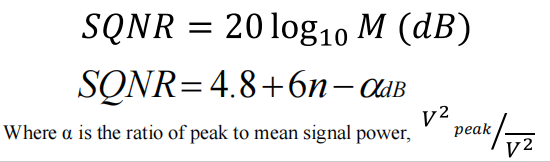
α is the ratio of peak to mean signal power(峰值与均值的电压差与均值的比的平方)
n是bit数
这个比率可以很好的描述出我们通信的质量,因为计算的是我们需要的信息(量化信号)和不要的信息(噪声)的比例。所以这个比例越高,说明通信系统越好,通信质量更清晰。
dB:
非均匀量化non-uniform Quantisation
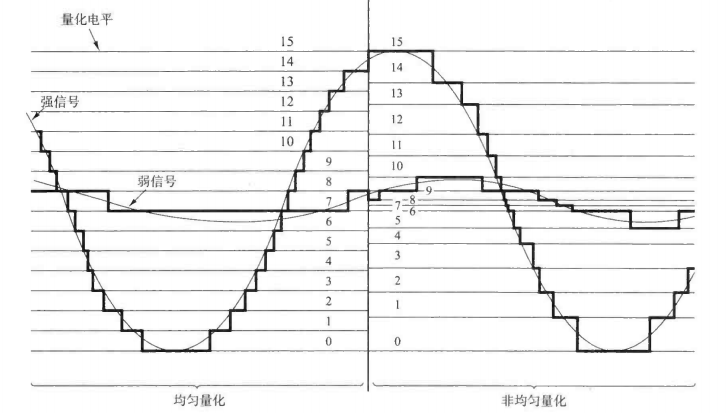
Non-uniform quantisation can provide fine quantisation of the weak signals and coarse quantisation of the strong signals.非均匀量化对弱信号可 以提供更精细的量化 ,而对强信号则采取较为粗糙的量化 ,因此可以通过非均匀量化使量化噪声与信号大小成正 比

Solution is to use nonuniform quantisation:
– Step-size varies with amplitude of sample.
– For larger amplitudes, larger step-sizes are used
– ‘Nonuniform’ because step-size changes from sample to sample.
principle
Nonuniform quantisation uses logarithmic compression and expansion.(对数压扩量化)
Compress at the transmitter and expand at the receiver.
Compression changes the distribution of the signal amplitude.
– Lower amplitude signals strength to higher values of quantisation
The logarithmic compression and expansion function is also called Companding(压扩 )

Pass x(t) thro’ compressor to produce y(t).
y(t) is quantised uniformly to give y’(t) which is transmitted or stored digitally.
At receiver, y’(t) passed thro’ expander which reverses effect of compressor.
Companding
There are two companding standards for telephony: A-law (G711a - used mainly in Europe) and µ-law(G711u - used in North America and Japan).
Implemented as a segmented, piece-wise linear
approximation.
- A率压缩曲线:
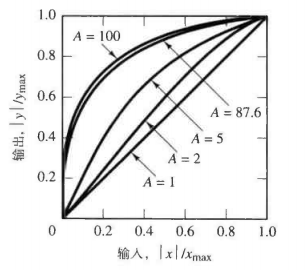
观察一开始的图像:强信号斜率大于1,而弱信号斜率小于1,通过压缩使强信号减弱,弱信号增强,都趋向于正比信号。
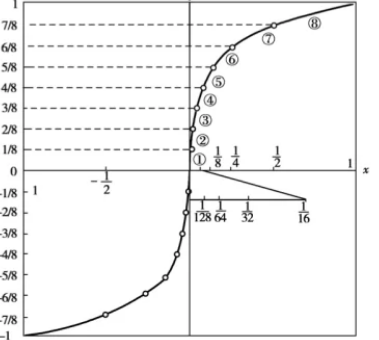
13-segment compression A-law十三折线法近似A率:
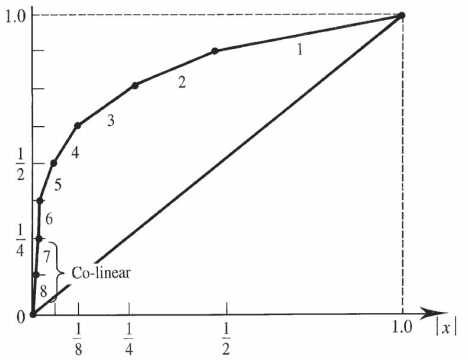
在正8段和负8段中,正1,2段和负1,2段斜率相同,合为一段。所以原来的16段折线变为13段折线,故又称A律13折线。
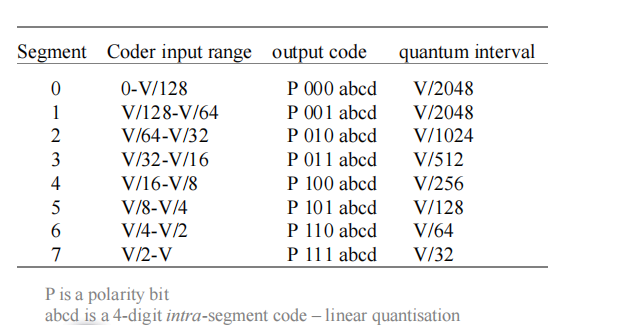
8-bit code consist of
– i) polarity bit P (range is ±V) 0正1负
– ii) 3 segment decoding bits XYZ (代表不同的segment)
– iii) 4 bits (abcd) specifying intra segment value on a linear scale (每个segment里均匀量化十六段)
调制modulation
采样、量化和解码是调制的重要步骤
PCM调制技术流程:
In pulse-code modulation (PCM) we can identify three components: sampler, quantiser and encoder.
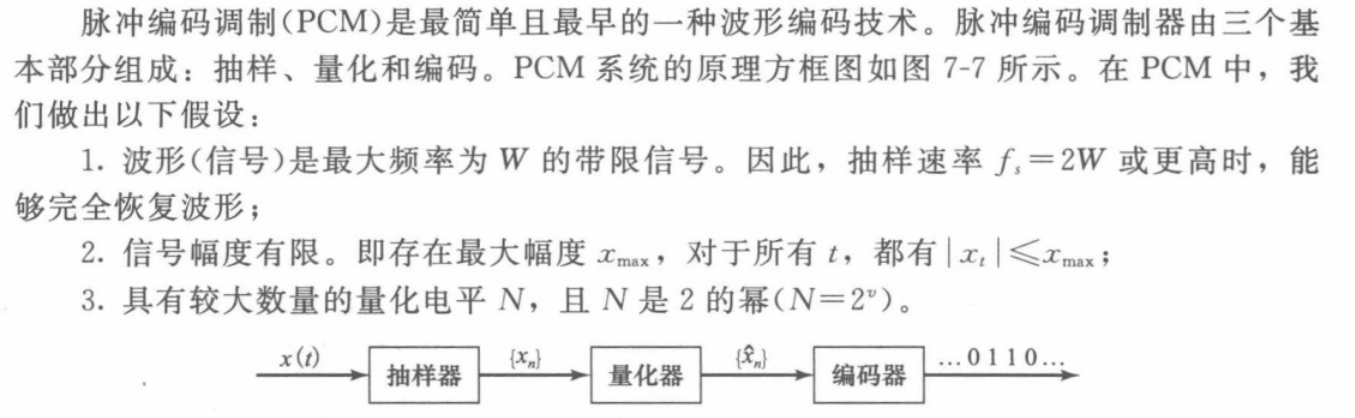
分为均匀PCM和非均匀PCM
bit rate
The encoder converts the sequence of quantized amplitudes into a sequence of bits. Hence, the bit rate 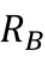 can be calculated as
can be calculated as
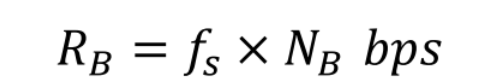
N是每个量化级别的比特数 fs是采样频率
Analogue & Digital Bandwidth
Analogue bandwidth of a medium is expressed in cycles per second (Hz).
Digital bandwidth is expressed in bits per second
Analogue bandwidth is the range of frequencies that a medium can pass.
Digital bandwidth is the maximum bit rate that a medium can pass.
Delta modulation (DM)
增量调制
Provides a staircase version of the message signal by referring to the difference between the input signal and its approximation
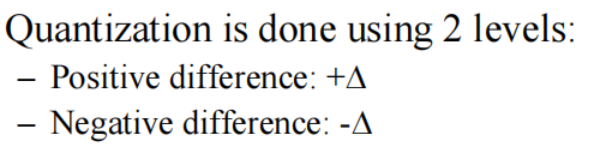
正Δ对应1,负Δ对应0
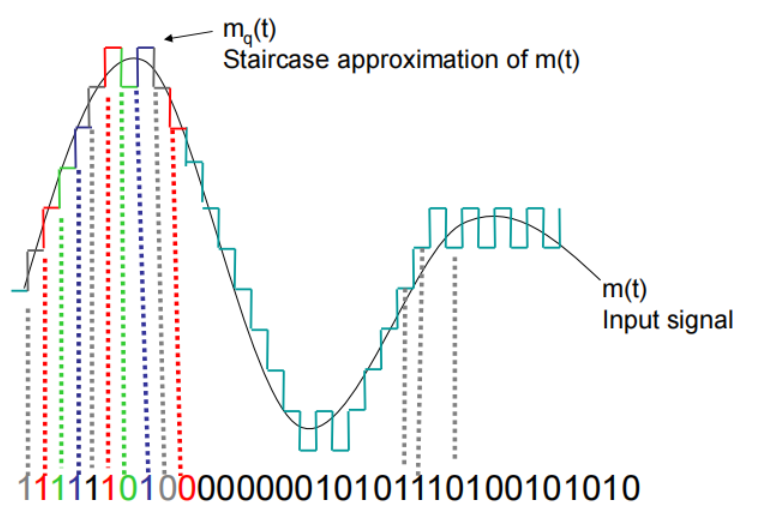
reciver 收到编码后,1则代表增加一个步长,0代表减少一个步长
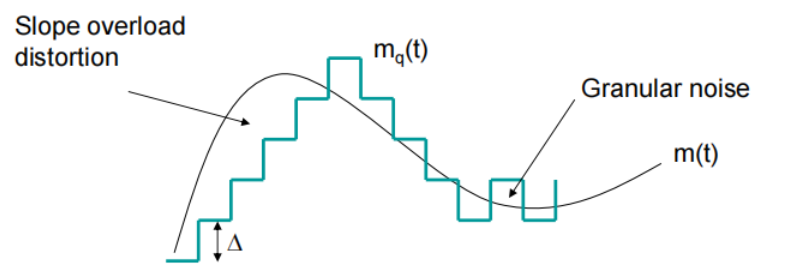
DM quantisation error
Slope overload distortion 斜率过载失真 输入变化太快
Granular noise 粒状噪声 输入变化太慢

信源 source
信源编码的目的:Used to compress the source so that it uses less resources in transmission – use Information Theory to do this
Memoryless source
Probability of an event occurring does not depend on what came before.
如果一个离散信源输 出的码元是统计独立的 ,则称该离散信源是无记忆性的(memoryless)。这
意味着如果同一时刻输出两个码元 ,则它们的联合概率密度可以由各自的概率简单相乘得到
Probability of a particular symbol is fixed
Sum of probabilities is 1
Source with memory
Probability of a symbol depends on previous symbol
如果一个离散信源各个分量之间是相关的,则称该离散信源是记忆性的。码元之间的相关性意 味着在一个M码元序列中,当已知前 M-1 个码元时,第M 个码元的不确定性就减少了

Lots of real sources in this category and coding like JPEG and MPEG exploits this to produce smaller file sizes

P(A;B)=P(AB)
Information theory
Information in communication.
– Signals: carry the information, a physical concept.
– Symbols(信元): describe the information by mathematics
Measure of information is a measure of uncertainty - more certain data contains less information.
定义信息量(information)I:
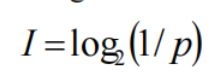
take logs to base 2 to get the units in bits.
信息量和码元出现概率成反比概率:
P=0 I=∞
P=1 I=0
Entropy(信源墒): the average information content per symbol
每个符号所含信息的统计平均值
单位是 bit/symbol
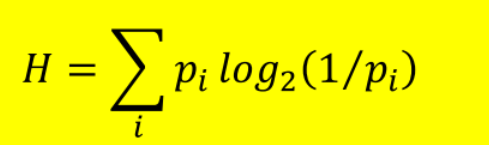

example:

Maximum Entropy: This occurs when all events have the same probability.
当每个码元等概率出现时,信源具有最大信息量,最大平均信息量(熵)为比特数
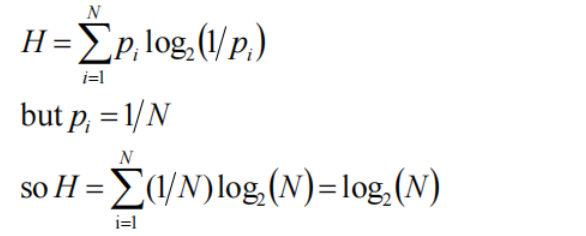
在example中需要传四个symbol,所以需要的比特数为2,也就是说 Maximum entropy= 2bits/symbol。
求得code efficiency=1.785/2=0.875 (87.5%)【因为要用2bit(通过编码长度加权平均算出来),但是每个比特传达信息的效率没有达到最高,所以需要coding】
Source coding:
Aims to reduce the number of bits transmitted
再看一个例子:

H=1.75 bit/symbol
还是ABCD四个symbol,但是对于这四个probability 编码不再只使用两个bit,而是按上述方式编码
这样做的好处是,使平均bit位数减少,从而提高code efficiency
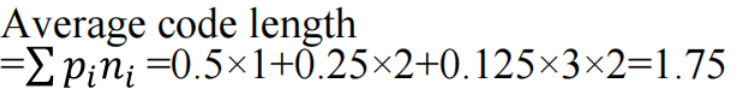
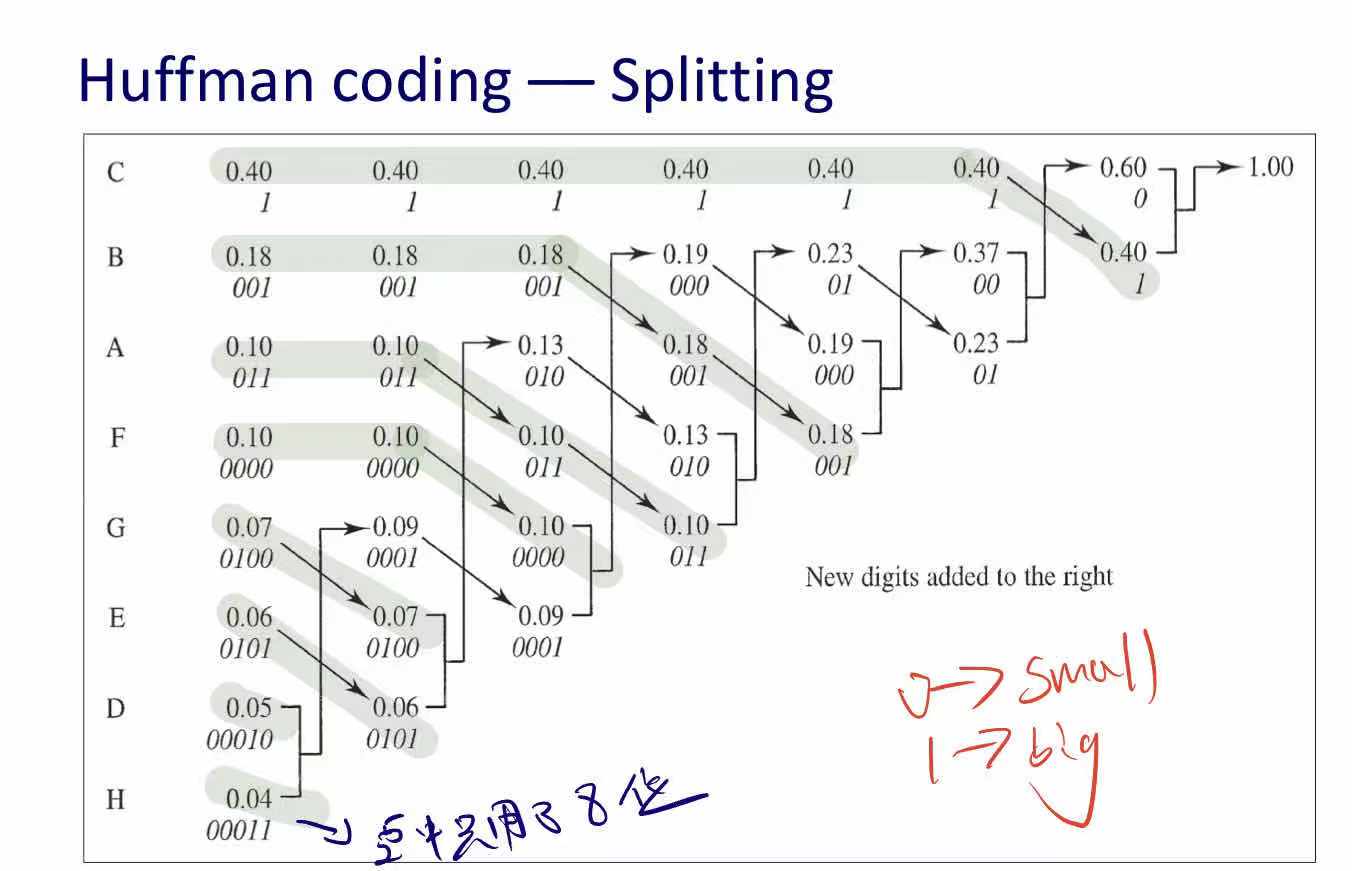
编码方式:Huffman coding
Put symbols in DESCENDING order of probability
Combine the lowest 2 and re-order
Repeat until only one value of “1”
Compression ratio= no source coding bits / average number of bits transmitted
Efficiency=H / average code length

DIGITAL CHANNELS
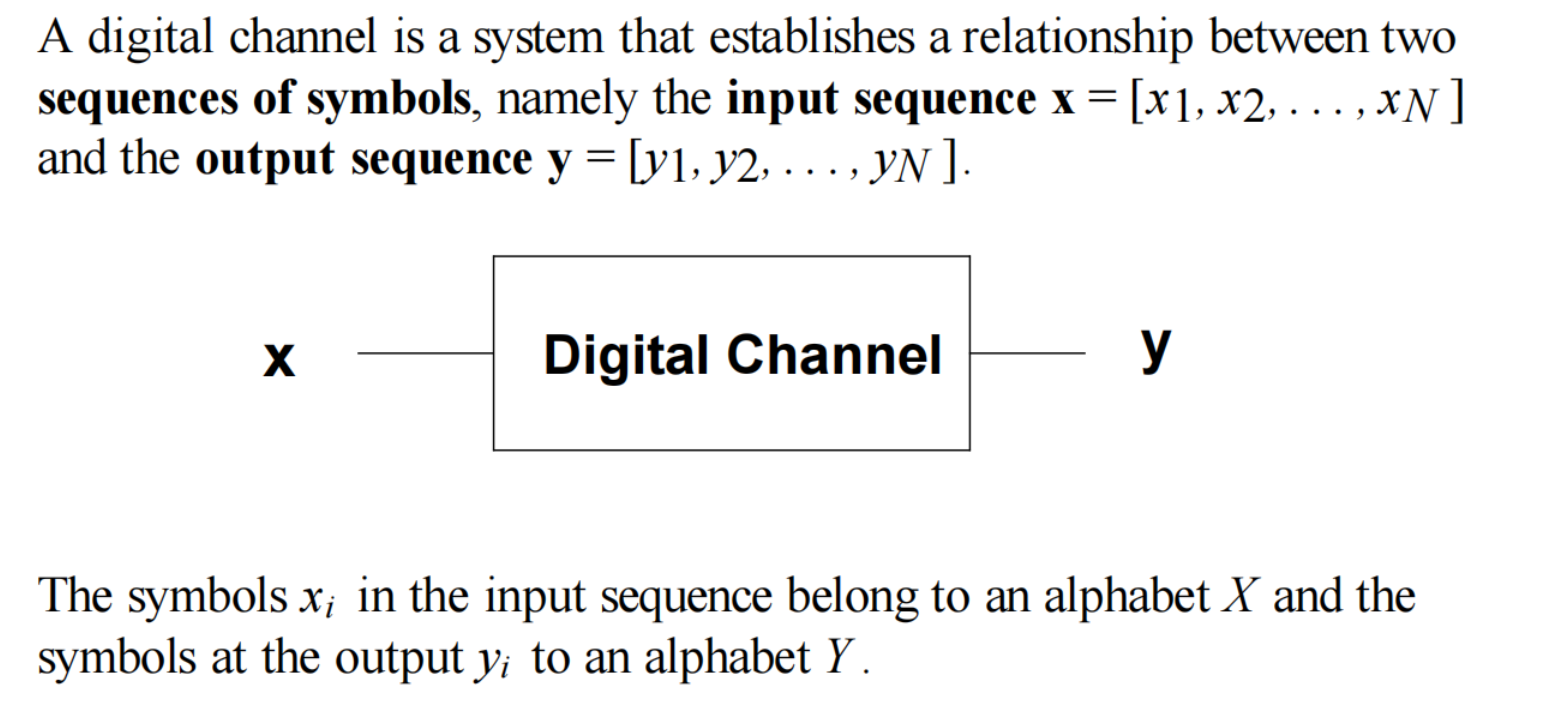
The digital channel is a mathematical abstraction. It describes the relationship between the sequence of symbols that leaves the digital channel encoder and the one that reaches the digital channel decoder.
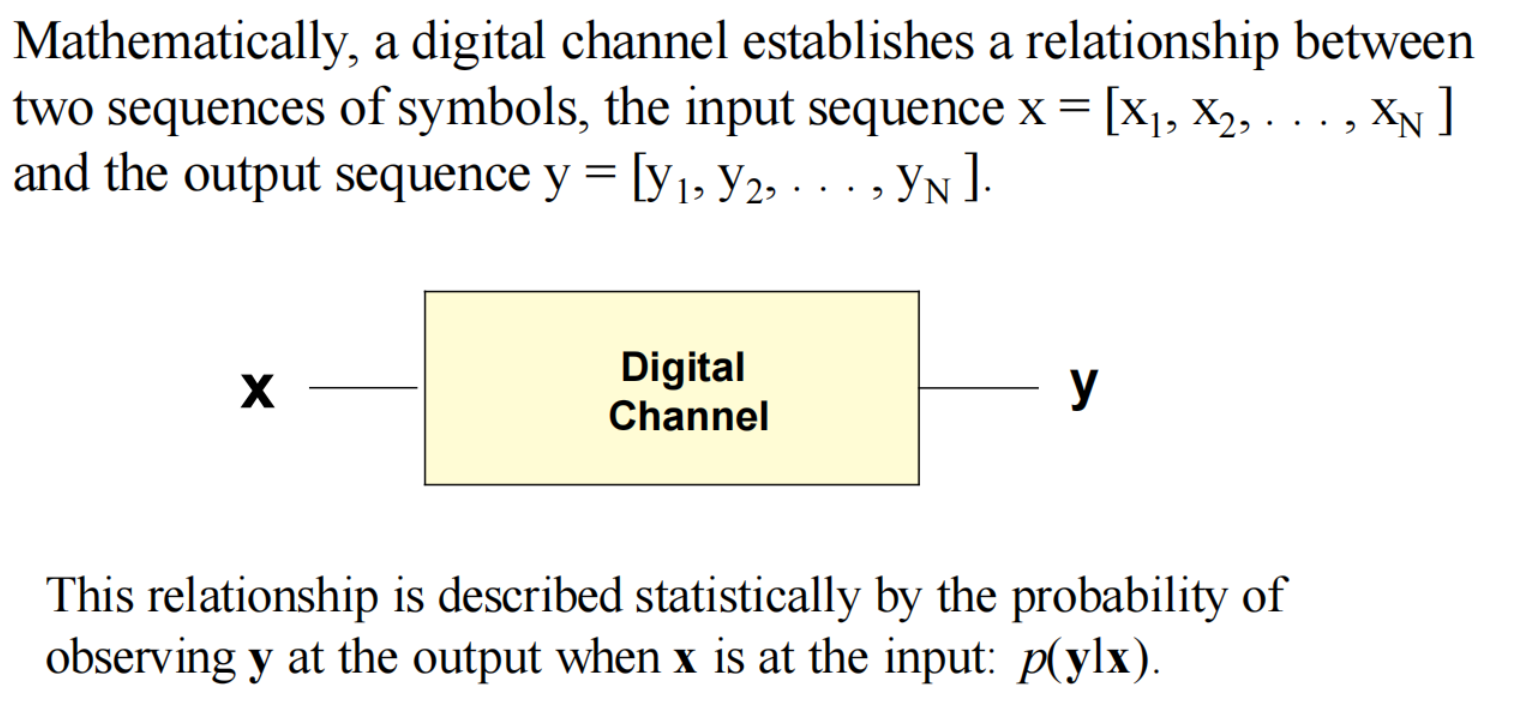
digital channel is an abstraction encompassing: (1) the modulator at the transmitter, (2) the physical medium and the (3) demodulator at the receiver.
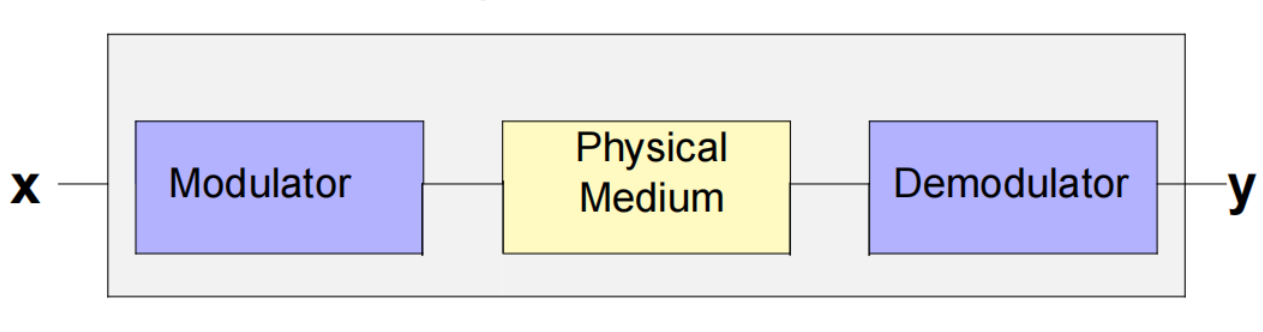
Hence, the modulator, the physical medium and the demodulator determine the relationship between the input symbol sequence x and the output symbol sequence y.
然而Y是不等于X的 因为会出现
Attenuation
Noise
Bandwidth limitations.
Multipath propagation
Mathematical definition of a digital channel
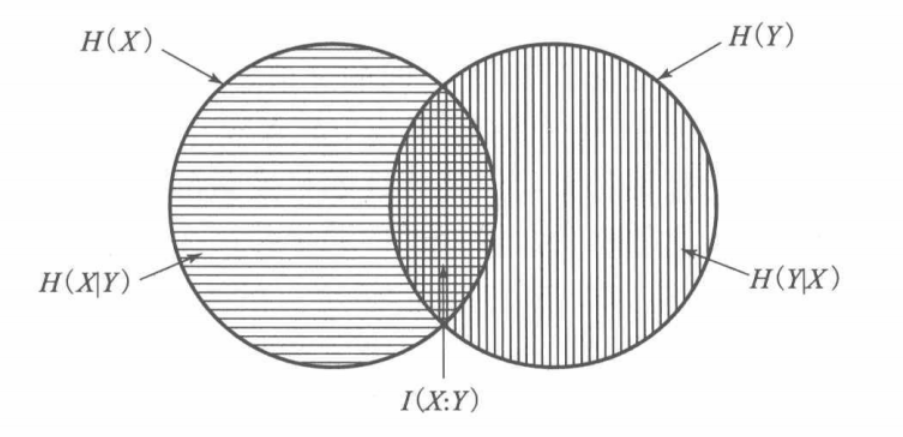
H(X) / H(Y) :the information content of each source
H(X, Y ): the information content of both sources.
H(X|Y) H(Y|X) : the new information provided by one source if the other source is known.
I(X;Y) : 互信息

0 ≤ I(X; Y ) ≤ min(H(X), H(Y ))
digital memoryless channel

A digital channel will be defined by a probabilistic relationship between the output and input sequence, namely the probability of observing y when we use x as the input, p(ylx)
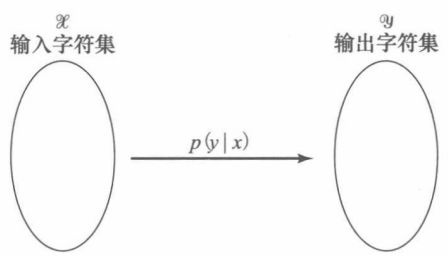
memoryless channels输出只取决于输入
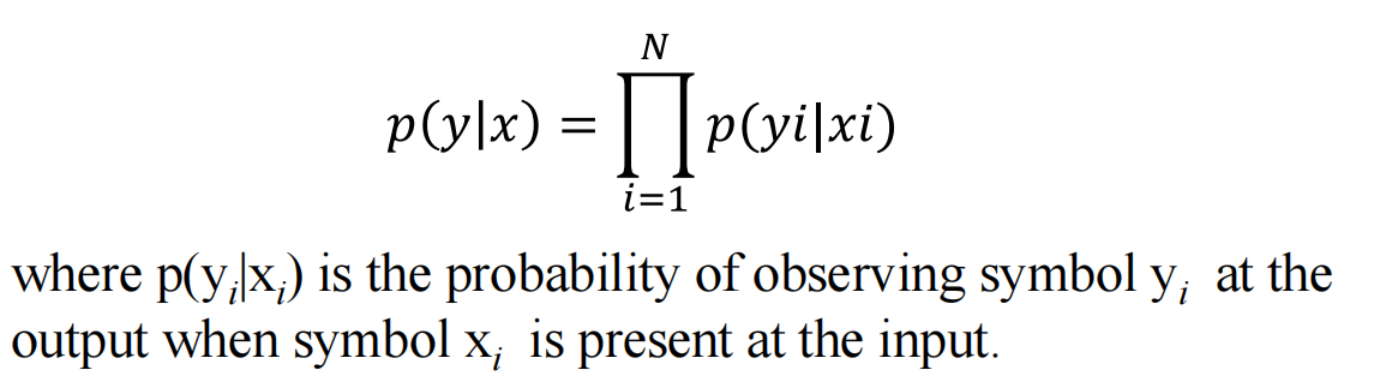
binary symmetric channel:
The binary symmetric channel is a special case of memoryless channelfor which the input and output alphabet are binary X = 0*,* 1 and Y = 0*,* 1and the symbol conditional probabilities are defined as:
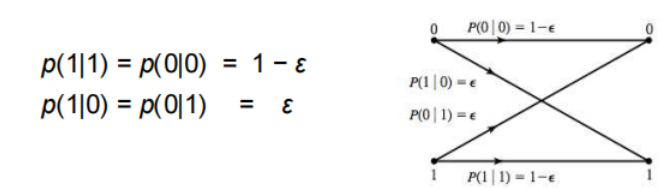
The value ɛ is known as the crossover probability. Note that p(1|0) + p(0|0) = 1 and p(1|1) + p(0|1) = 1.
Additive white gaussian noise (AWGN) channel
Binary PAM is the simplest digital modulation method. Symbol 1 is converted into a pulse waveform S1(t) of amplitude A, whereas symbol 0 is converted into a pulse waveform S2(t) of amplitude −A
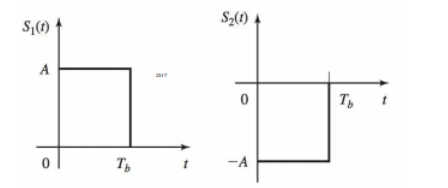
利用模拟信号当作载波传递数字信号:A->1;-A->0
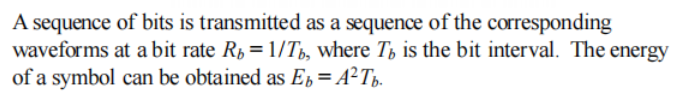
output r(t) can be expressed as the message signal at input sm(t) plus white gaussian noise, n(t)
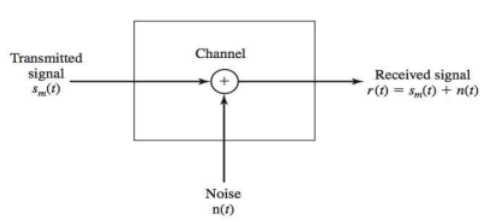
r(t)不是y(t),y是r(t)经过demodulate后的信号
The binary PAM demodulator consists of three steps, namely a matched filter, a sampler and a detector.
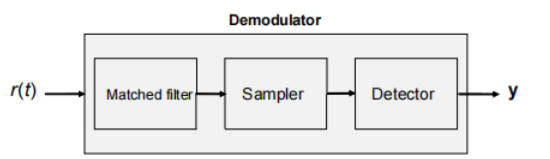
匹配滤波器将输入波形与预期波形进行比较。采样器提供了接收波形与预期波形相似程度的数值。基于这个值,检测器将决定是接收到符号1还是符号0。
一个问题:这个检测器的判断标准是什么?难道大于0就应该1;小于0就应该是0吗
看这张图:在传播过程中以矩形波为载体,到达demodulation端后,由于信号的损失可能信号已经变为红线这样,在对其进行采样+量化 ,所以量化标准是什么?是否是上个问题那样
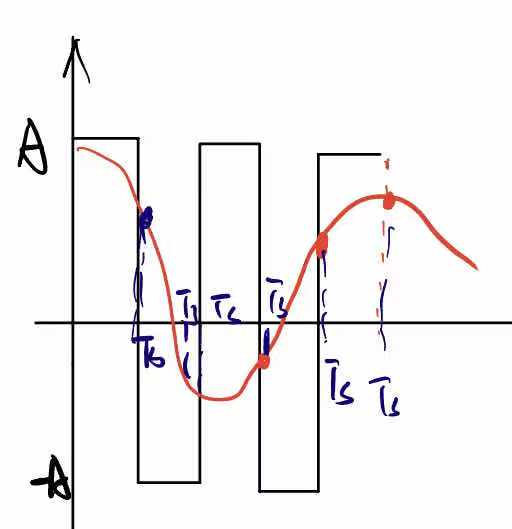
回答:根据统计这样有一定错误概率
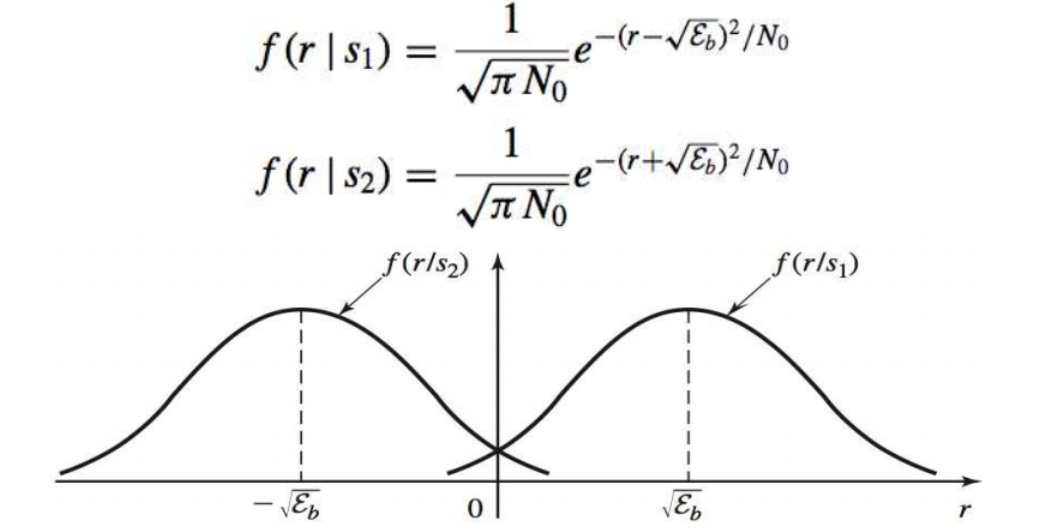
这个图是r(t)的概率分步曲线可以看到在r<0的部分仍有可能将y判断成1.
所以判断错误的概率是
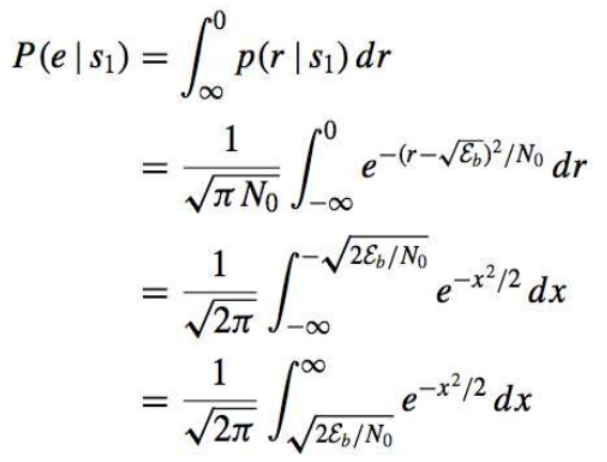
Channel capacity
The main objective when transmitting information over a channel is reliability, which is measured by the probability of correct reception at the receiver.
Information theory tells us that this probability can be increased as much as we want as long as the transmission rate is less than the **channel ** capacity.

The channel capacity imposes(施加) a theoretical limit on the transmission speed. Hence, the probability of error affects the speed of the communication
信道容量在传输速率上施加了一个限制,这个限制就是channel capacity(是与错误率有关的)
首先是一个例子:
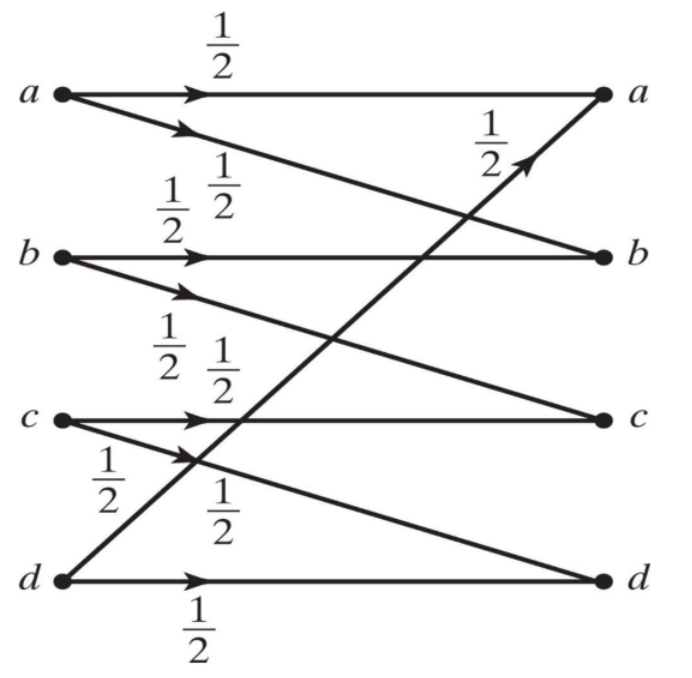
现在有一个四输入四输出的离散信道,如果发送方发送a有几率会在发送过程中变成b, 同理如果接收方收到b它也无法判断这个b是否是真实的b传输而来(或者是a发生了错误)。这就是我们说的不确定性,也就是说不能进行可靠的信息传递。
为了进行可靠的信息传递,我们必须牺牲掉一部分输入(只用字符a c通信 则接收方收到a/b都可以认为源信息是a)这就消除了不确定度。值得注意的是我们选择传输symbol的时候要确定他们对应的输出是不为相交的,这样才不会产生信息的不确定性。Using only those inputs whose corresponding possible outputs are disjoint, and thus do not cause ambiguity
Channel capacity of Binary Symmetric Channels
Let us consider a memoryless binary digital channel with input sequence x= [x1*, x2, . . . , xN* ] and output sequence y = [y1*, y2, . . . , yN* ]. Let ɛ be the crossover (error) probability.
这里x1,x2是symbol(相当于上图中abcd)
For N large enough, we will expect N × ɛ errors in the output sequence y. 当N足够大时,我们预计输出序列中会有N × ɛ个错误
Using Stirling’s approximation for factorials, the number of possible output sequences y that disagree with x in N × ɛ positions is
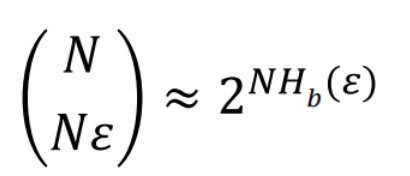
where Hb (ɛ) = −ɛlog ɛ− (1 − ɛ) log(1 − ɛ).
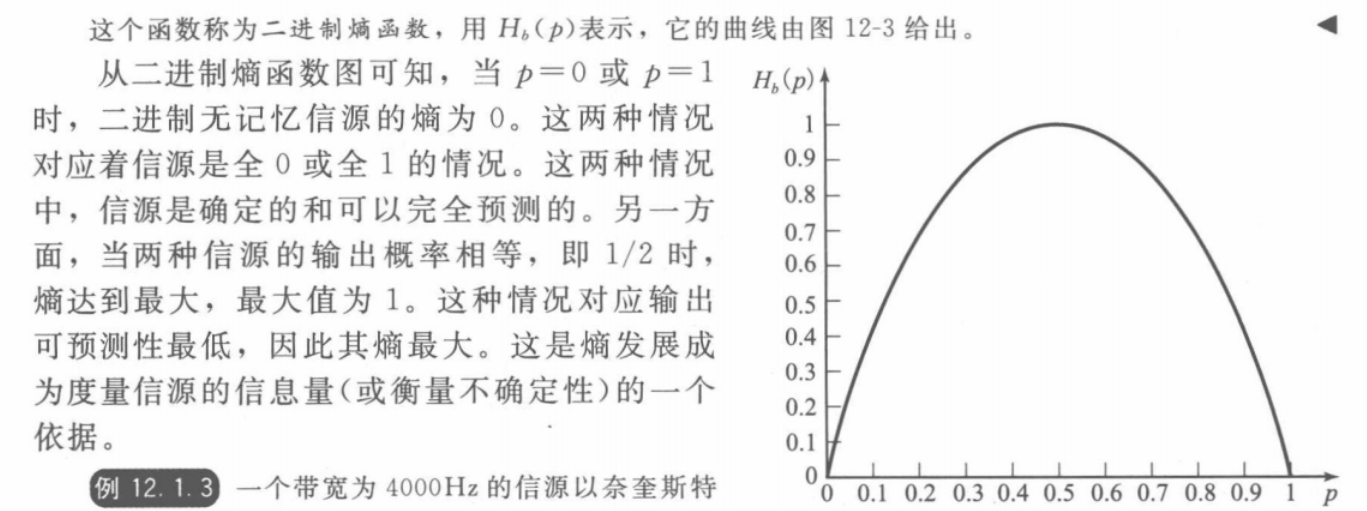
This means that for every input sequence x of length N there will be approximately 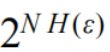 different
different
output sequences y of length N N个X对应 个y
个y
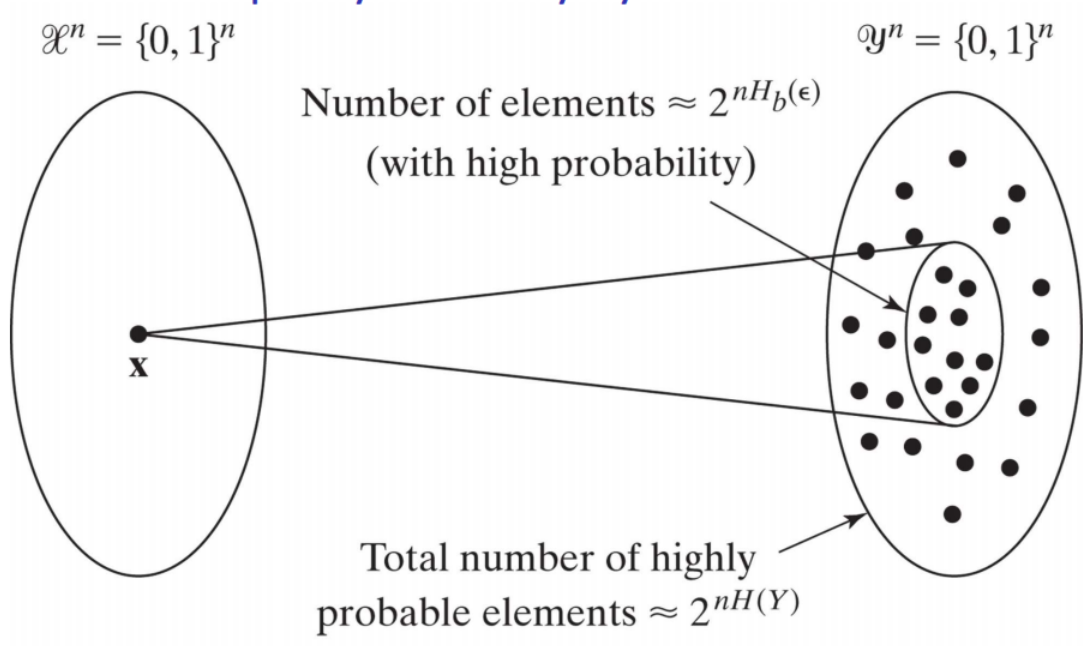
x(一个sequence)可以映射到y中多个字符(类比于开始时那个例子里a对应到y处的a和b)
所以说一个小圈里的sequence数目是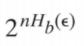 有趣的是H(ɛ)是由信道自身属性决定,所以每个圈里sequence个数是一样的
有趣的是H(ɛ)是由信道自身属性决定,所以每个圈里sequence个数是一样的
一个大圈里的sequence数目是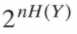
Hence, the maximum number of input sequences that produce almost non-overlapping output sequences is at most equal to
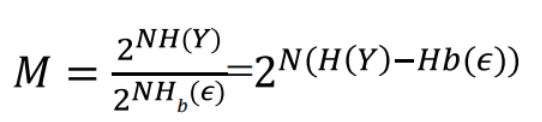
(N是Y的数目,M是可以使用的X数目(N减去舍弃的X的值))
Then, in theory, if we choose wisely M **different input sequences **we can always identify them without error by looking at the output sequence.
If we restrict ourselves to M different binary input sequences of length N , the transmission rate R will be:
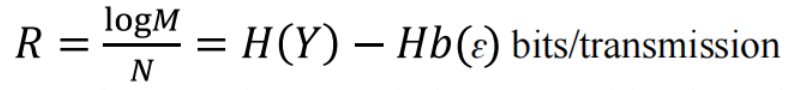
How can we increase the transmission rate? Either by reducing Hb (ɛ)or by increasing H(Y ):
The quantity Hb (ɛ) cannot be controlled, since it is a property ofthe channel.
The entropy H(Y) can however be maximized by wisely choosing p*(*x).
P(x)等于0.5时H(Y) max=1( H(y)max=所用比特数,因为这里binary symmetric channel所以只有两个状态且是等概率,信源熵达到最大1)
binary symmetric channel capacity: The resulting maximum transmission rate C will be: C = 1 − Hb (ɛ) bits/transmission
最大传输速率与ɛ的关系
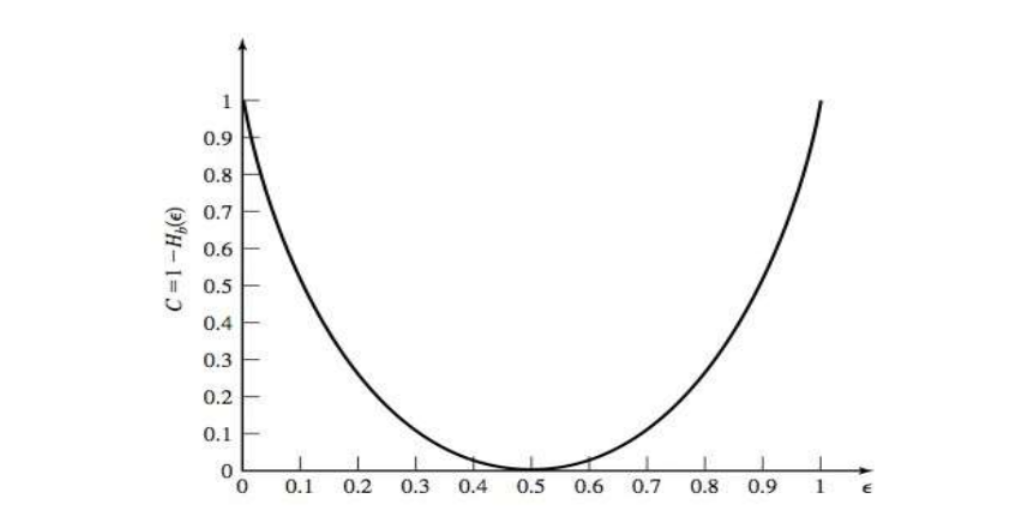
显然只是二进制熵函数颠倒: 0和1不确定性最小所以说明容量最大,0.5时不确定性最大,容量也最小
The Noisy Channel Coding Theorem
互信息是y已知情况下x减少的不确定性,所以如果可以选择p(x)使x不确定性减少到最大,此时信息传输最多,传输率为C
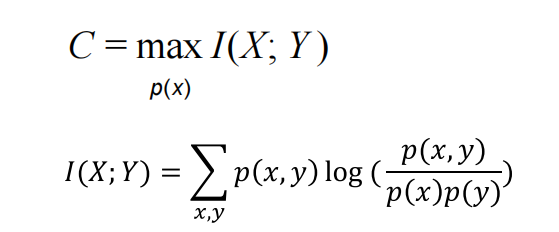
max下面的P(x)意思是当取到最合适概率时,是信道容量
可以理解成A-B在某信道上通信,A给B的传达的信息量在信道收受干扰会丢失,丢失之后,B最终得到的每个信号上的有效信息,是互信息量(bit/symbol),最大化互信息量可以达到信道容量,即传送信息的最大能力,如果高于这个值去传输信息,会产生大量错误。

If the transmission rate R is less than the channel capacity C, therewill exist a code that will result in an error probability as small as desired. If R > C, the error probability will be bounded away from 0.
CAPACITY OF AWGN CHANNEL
additive white gaussian noise
Shannon’s formula
Only when the information rate is below the capacity of the channel,error-free transmission can be achieved
According to Shannon’s formula, the capacity of an additive white Gaussian noise channel is
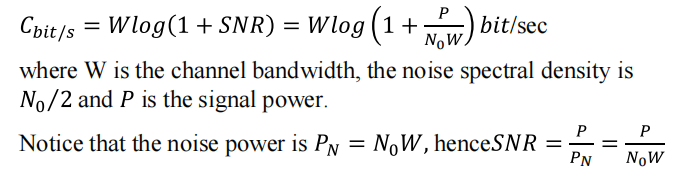
- SNR信噪比:信号的功率比噪声的功率
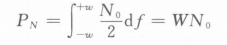

In digital systems, the speed of communication is measured by the bit transmission rate RB (number of bits per second) or, in general, by the symbol transmission rate RS(number of symbols per second)
the maximum symbol transmission rate is 2W symbol/s
所以也可以使用这种形式表示:
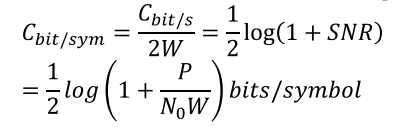
Consequently, we can measure the channel’s capacity both in bits/sec and bits/symbol
从公式看,C与W和SNR有关,下文介绍这两个参数对C的影响
Signal to noise ratio(SNR)
信噪比
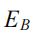 is the average energy that we use to transmit one bit
is the average energy that we use to transmit one bit
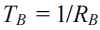 is the duration of one bit
is the duration of one bit
Rb是bit/s
信号功率可以表示为: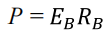 每秒每传输一比特的功率
每秒每传输一比特的功率
所以信噪比可以表示为:
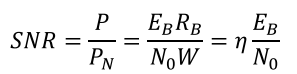
η
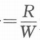 是 spectral efficiency 带宽利用率
是 spectral efficiency 带宽利用率η is used to measure how efficiently the available bandwidth is used. It is defined as
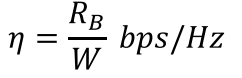
and Shannon’s formula as
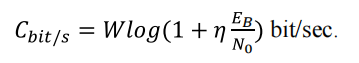
Bandwidth effects
With higher bandwidths the transmission rate can be increased. However, higher bandwidths also imply higher noise power. The following limit can be derived:
增加带宽,可以使信道每秒传输更多的抽样信号,增大了传输速率,但从另一方面来说,也会增大噪声的功率,当W趋于无穷大时,信道容量为:
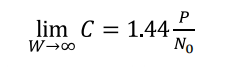
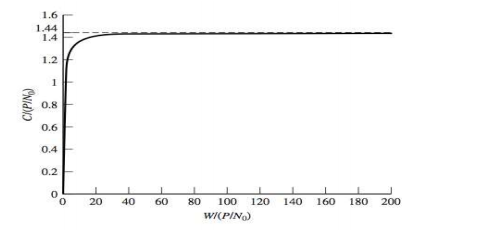
所以仅仅通过增加信号带宽不能将信道容量增大到任意值
SNR effects·
By increasing the signal to noise ratio (SNR) the maximum information rate for reliable communications increases.
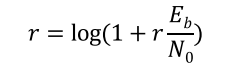
(Shannon formula 两边同除w)
图中r与η相同:为spectral efficiency(带宽利用率)
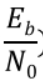 是每bit信噪比
是每bit信噪比
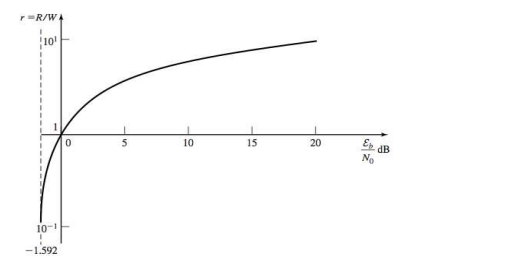
这里两个参数分别为,纵轴:频谱比特速率,横轴:每比特信噪比。分别衡量带宽效率和功率效率。
CHANNEL CODING
Coding is a process that produces a sequence of symbols from another sequence of symbols.
In source coding, given a sequence of symbols we produce a new,shorter sequence that contains the same information. Hence,eliminate redundancy
信源编码的目的:信源输出符号序列变换为最短的码字序列,使后者的各码元所载荷的平均信息量最大
channel coding our aim is to protect informationagainst errors and for that we introduce redundancy, producinglonger sequences of symbols.
信道编码的目的:就是在发送端对原数据添加冗余信息,这些冗余信息是和原数据相关的,再在接收端根据这种相关性来检测和纠正传输过程产生的差错。(冗余是可靠的代价,我认为可以理解成前面信道建模时候把M个x编到N个)
在信源编码中减少不必要的redundancy,在信道编码时我们又加入合适的redundancy.
Coding rate
Let k be the length of the original binary sequence and nthe length of the sequence after coding. Hence, we are introducing m = n − k redundancy bits
k个信息位,n-k个冗余(校验位),根据某种数学关系构成长为n的码字,码率为k/n
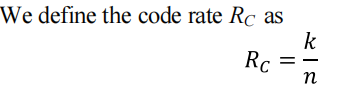
2的n次种序列中只有2的k次是有效的码,如果收到不是这2的k次中的组合,则意味出现错误
Effects of coding on the bandwidth and the bit rate
信道编码对带宽的影响:RC = k/n
如果bandwidth是固定的,那么n the information rate will decrease by RC
如果信息传输率是固定的, the transmission rate will increase by 1/RC and so will the necessary bandwidth
Error detection and correction
两种纠错方式:
FEC:Forward error correction:protects our messageagainst up to NC errors.
错误数小于Nc的情况下接收方自动纠错(比如说0编码为000错误为001,接收方认为001也是0意思)
Automatic repeat request(ARQ) consists of asking the sender to retransmit the message
For the same code rate RC , ND > NC
Types of channel codes
Block codes. In a block code, an information sequence isbroken into blocks of length k and each block is mapped intochannel inputs of length n. Each block is independent fromany other block
Convolutional codes. In a convolutional code, k bits of theinformation sequence enter a k × L shift registry. The bits are linearly combined to produce n bits. Hence, each n-bitoutput depends on the previos k × (L − 1) bits. In other words, convolutional codes have memory
linear block codes
An (n, k) block code C = {c1*,* c2 . . . , cM} is defined by a collection of M = 2^k binary sequences of length n called code words. Instead of sending the original block of k bits, we send a code word.
code words:编码后的信号

Definition: A block code is said to be linear if any linear combination of code words is also a code word.
linear combinations are defined as the component-wise modulo 2addition (i.e. 0+0=0, 1+1=0, 1+0=1, 0+1=1)
zero sequence 0 is always a code word of any linear block code

可见这四组为线性编码
Hamming distance and Hamming weight

hamming距离:两个码之间不同的位数
hamming权重:码中1的个数
对于线性分组码,除去全0.最小hamming距离为最小码重
In the previous example, the Hamming distance between code words01111 and 10100 is d(01111*,* 10100) = 4. However, the minimum distance of the code is dmin = 2.
Hamming distance
Given an output sequence y, we can obtain the distance between this sequence and all of the code words 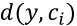
hamming 距离与纠错的关系:

Generator matrix
any information sequence x can be mapped into its code word c by multiplying it by the generator matrix G
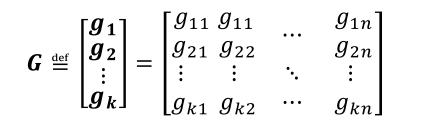
编码过程: c = xG.
It is easy to see that the code word for the sequence10 . . . 0 is g1, for 010 . . . 0 is g2 and so on,所以信息源为10000…的码字就是纵向的g1,01000…码字是g2

Systematic codes(系统码)
前k位为信息位,后n-k校验位
In a systematic code, the code word consists of the information sequence followed by a sequence of m = n − k bits, known as the parity bits.
所以可以得到 the generator matrix has the form
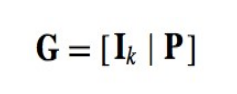
用x×g可以保证前k位还是原始信息bit
Parity check matrix
校验矩阵
The parity check matrix H allows us to check whether a code word belongs to our code or not. It has the property that
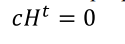

If the code is systematic, the parity check matrix can be obtained as
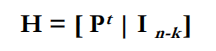
- example:
P的转置是H的左半部分
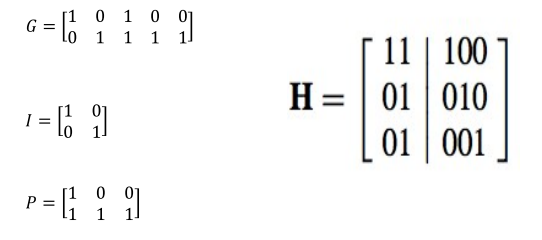
Principles of block decoding
译码过程: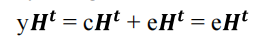
During decoding we essentially **compare each received sequence with all the code words defining the code and then **choose the most similar code word.
如何定义相似性?接收端如何能认为一个发生错误的码字本身为某个信息源码
syndrome decoding
校验子
Let us denote by e the error binary sequence. The output sequence y that we obtain when code word c is transmitted can be expressed as
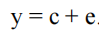
y是接收的码字,c是编码后的码字,e是错误图样
If there are no errors during transmission, e = 0, if there is an error in the first bit, e = (10 . . . 0), if there is an error in the first and third bite= (1010 . . . 0), and so on.
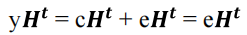
Notice that the result of this operation depends on the error sequence e and not on the code word c that we have transmitted(因为
为0)
定义行向量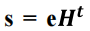 为syndrome
为syndrome
s is a 1 × m vector and there will exist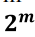 different syndrome sequences s.
different syndrome sequences s.

relate an error sequence e to one syndrome sequence s, we can determine e based on the calculation 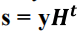
c = y + e
译码过程
根据以下算法列出所有可能的伴随式与错误图样的对应关系

比如:
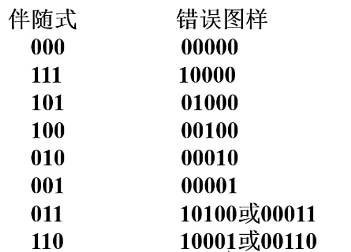
接收方收到y,通过校验矩阵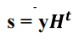 算出s再找s与错误图样的对应表(事先算好),然后可以得到e再用c=y+e得到准确的码字
算出s再找s与错误图样的对应表(事先算好),然后可以得到e再用c=y+e得到准确的码字

Hence, we need as many syndrome sequences s as error sequences e we want to identify.
if we want to be able to correct onesingle error in our sequence we need
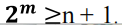
s的总数大于n+1









