DFT-S-OFDM
DFT-S-OFDM
记录一个小项目学习过程
传统OFDM功率均峰比较大,采用DFT-S-OFDM降低均峰比
预备知识
多址和复用(FDM)

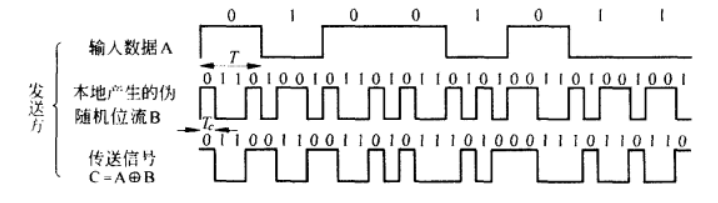
直接扩频
使用扩频码和原始信号相乘以此得到更高频率的信号
原理
DFT-S-OFDM是在OFDM内增加DFT扩频操作,以此减小PARR
OFDM的调制框图

在串并转换后添加DFT扩频以此实现DFT-S-OFDM
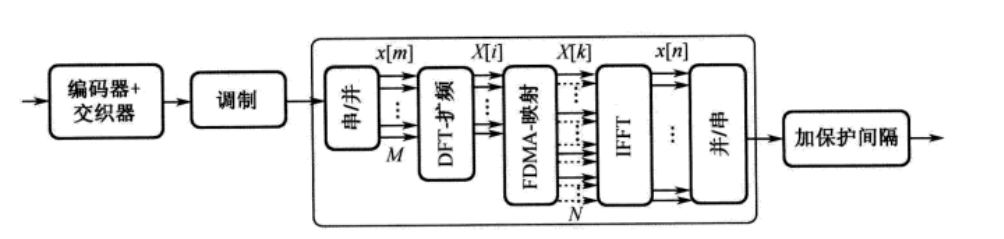
有意思的是如果DFT扩频序列的长度与IFFT相同,二者作用可以抵消,此时等价于使用SC-FDE.
DFT-S-OFDM之所以被称为单载波OFDM是与它前面对数据块做DFT变换的点数M和进行OFDM调制的IFFT点数N有关,一般N>M;当N=M时,信号直接调制到子载波上,FFT和IFFT作用互相抵消,信号就直接在时域上进行传输;当N>M时,经过DFT变换,在IFFT处理之前,每个子载波上的数据己不再是独立的源数据,而是各个源数据的叠加,相当于每个源数据扩展到了多个子载波上构成单载波,信号映射到子载波上进行OFDM调制,其中N个子载波上有输入数据。
在时域看来,输入数据的符号持续时间T在经过SC-FDMA调制后变为:T=(N/M)*T
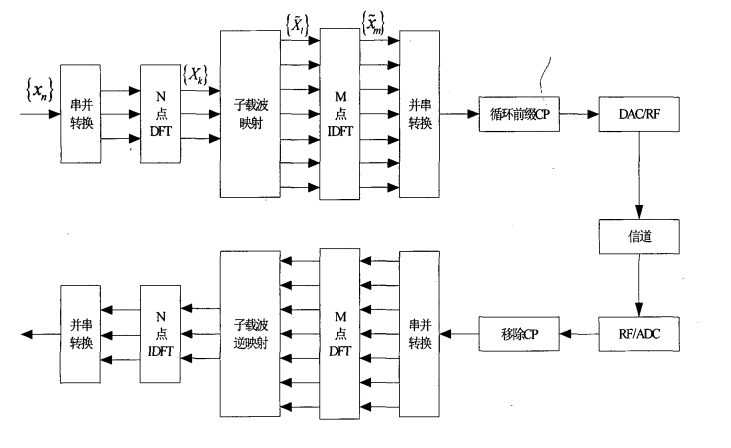
DFT扩频
参数:M是DFT输出个数,N是IFFT输入个数,S=N/M是带宽扩频因子
分布式FDMA和集中式FDMA
分布式FDMA是指:均匀把DFT结果分派到子载波上,并且其余N-M位为0
集中式FDMA是指:只在中间相邻位置将DFT插入。
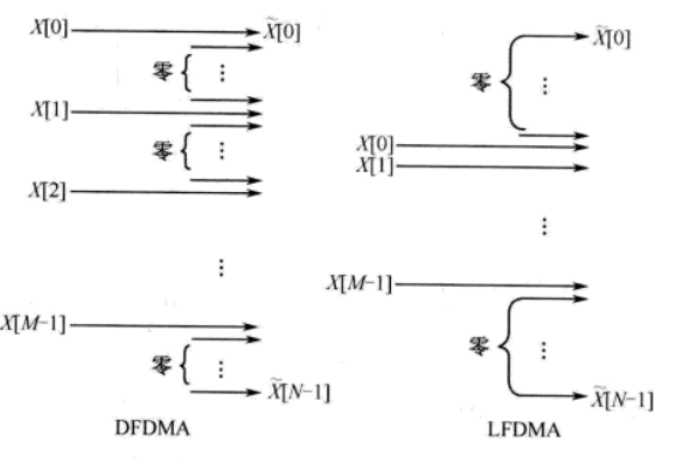
本项目采用另一种FDMA方式:
扩频数学表示
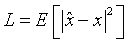
$\widetilde{X}[k]$ 是IFFT的输入,将其做n点的IFFT
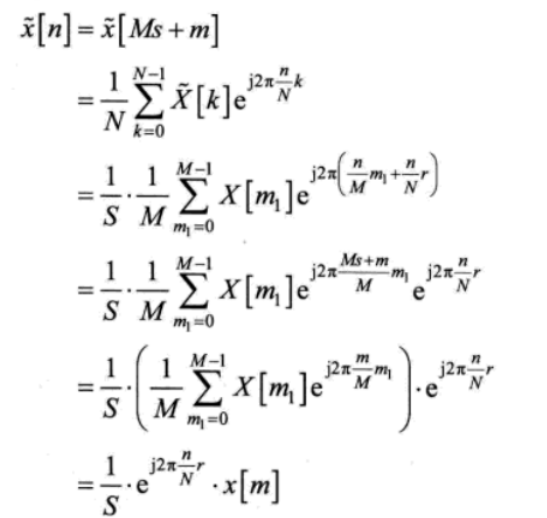
有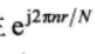 的相位偏移
的相位偏移
设计流程
处理流程
整个接收端大体上可以分为3个部分,分别是定时同步与帧同步、频偏估计与补偿、信道估计和均衡与解调。
对每一帧信号,接收机都先从空闲状态开始捕获帧头,即在2倍过采样上对长度为16的完美序列进行并行相关,寻找相关峰值。在捕获到帧头后,在8倍过采样上挑选最佳样值供后级模块使用,然后进入帧同步状态,检测前导序列中的序列翻转位置,结合最佳样值和序列翻转位置即可获得准确的同步位置。
此后,接收机开始进行频率估计,获得频偏估计结果并对后续的接收信号进行补偿。在每个子帧导频的CP段(循环前缀),都再当前最佳采样附近重新进行最佳样值选择,并在选择结果的控制下将做完频偏补偿之后的数据经过FIFO缓存送入去CP、FFT变换模块,再将导频部分、数据部分分别送入信道估计和频域均衡与解调模块。
信道估计模块接收256个符号长度的导频部分的FFT变换结果,在频域上对梳状导频点上进行信道估计,并使用线性插值方法得到频域各个点上的信道估计值,利用导频点以外的其他点的频域值进行噪声方差的计算,将512个符号长度的信道系数估计值和噪声方差估计值送入频域均衡与解调模块。
频域均衡模块对子帧中的6个数据块进行均衡。每个数据块首先做FFT转换到频域,利用对应点上的信道估计结果在频域进行信道补偿,然后再做IFFT转换到时域,并分别取I、Q路的符号位完成解调。
帧结构
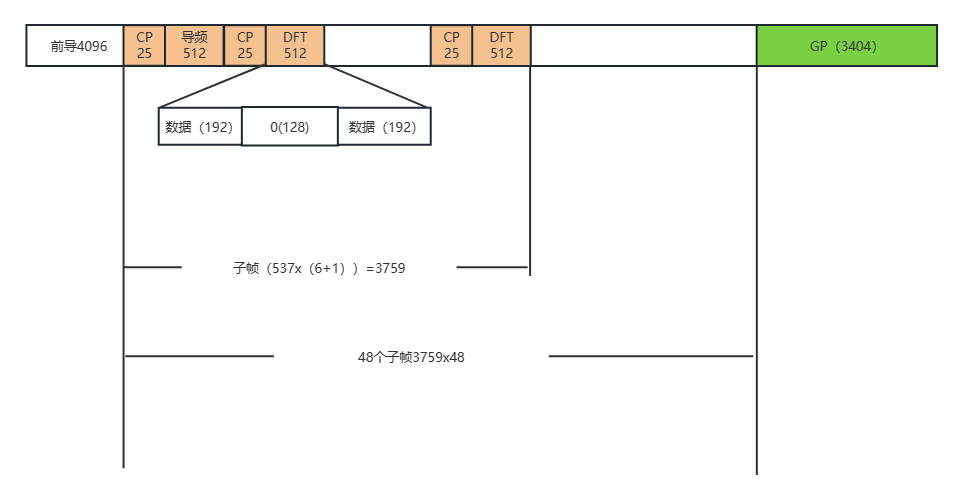
采用基于块的传输方式,每个数据块前面需要加上循环前缀,循环前缀的时间长度需要大于多径时延
为了实现相干解调,数据帧中需要插入导频,为了获得良好的信道估计性能,我们采用256长度的导频,由于一个帧内分为50个子帧
因此,每个子帧包含1个长度为247符号的跳频切换块,由1个长度为(25+256)导频块以及6个长度为(512+25)的数据块组成
前导序列占用4096个符号
*位同步方案*
在无线通信系统的实际工作过程中,接收端在开机后并不知道接收到的信号从何时起为有用信号,也不知道接收数据的位置,因此要进行接收机后续模块正常的信号处理流程,就需要通过位/帧同步来确定每帧数据的起始位置,从而提取对应位置的数据块。
相关检测是一种定时同步方法,它是根据序列良好的自相关特性来进行同步,相关检测算法是将本地存储的序列与接收信号做相关运算,寻找相关峰出现的位置,获得粗略的位同步。
并行相关是相关检测算法的一种,并行相关是用多个相关器并行进行相关运算,同时对训练序列的不同相位进行相关积分运算。并行相关将所有可能的序列相位同时相关运算,从时间上来讲性能非常高,适合于突发帧传输系统。但是,当训练序列周期如果很长,并行相关实现复杂度就会很高。
本系统选择长度为16的完美序列重复发送构成前导序列用来完成接收端的同步,相关检测算法选择并行相关,并行相关器个数为16,同时对2倍采样的信号进行相关操作。该完美序列为s1= [1+j, 1+j, 1+j, 1+j, 1+j, -1+j, -1-j, 1-j, 1+j, -1-j, 1+j, -1-j, 1+j, 1-j, -1-j, -1+j]。该完美序列的周期自相关
该完美序列的周期自相关特性如下所示,除了相位完全对正的情况出现明显之外,其他位置的相关值均为0。
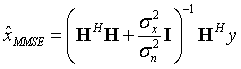
图 2 6完美序列的周期自相关特性
系统接收端收到的是八倍过采样数据,位同步模块先任意选择其中间隔为4的两路数据(比如0,4路)分别送入两个匹配滤波器,每输入一个样值都可以得到一个滤波输出,对滤波输出的I路和Q路的绝对值相加,称为相关值,记忆连续15个相关值并求和,当一个新的相关值与前14个相关值的比值大于门限值时,则认为捕获到信号,也就确定了完美序列的相位。
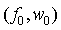
接着,进入最佳样值选择和同步验证阶段。同步验证的目的是为了避免冲激噪声使前一步骤同步捕获过门限,发生虚警。验证方法是对连续的4个周期继续进行匹配滤波,在前一阶段过门限的位置求出当前相关值和之前14个相关值之和的比值,如果4次所求得的比值都能超过门限,则认为同步成果,否则,则重新进入捕获状态。
最佳样值选择是在前一步过门限的样值位置基础上,对连续8个样值位置上的相关值进行比较,从中找出大值出现的位置,即为8倍过采样中的最佳样值。

图 2 8确定最佳样值流程
帧同步方案
位同步只是在符号和样点上同步上了,但帧的起始位置还存在模糊问题,为了接收端后续模块的工作,需要进行帧同步。
前16个完美序列周期和后240个完美序列周期相位相反,我们利用前导序列的这一特点来实现帧同步。
帧同步的原理是假设信道变化较慢,相邻的两个完美序列周期所经历的信道不变,那么我们可以对相邻两个完美序列周期的相关值进行共轭相乘,如果相乘的结果为负数,则可以认为这两个周期的序列之间相位发生了突变,
前一个完美序列周期的相关结果:
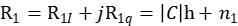
如果无跳变,后一个完美序列周期的相关结果为:
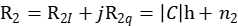
如果有跳变,后一个完美序列周期的相关结果为:
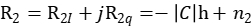
对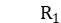 和
和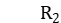 做共轭乘,可以得到:
做共轭乘,可以得到:
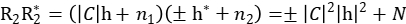
N表示包含噪声的各项之和。
这样,我们通过确定出当前的完美序列在前导序列中的位置,也由此确定了各个数据样点在帧结构中的位置,完成帧同步。
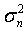
图 2 9帧同步原理示意图
频偏估计方案
由于通信信号受到多普勒效应、接收端和发送端晶振频率不匹配等因素的影响,接收信号的载波频率偏离了接收端的本地振荡频率,导致接收信号在本地振荡频率完成下变频后,通常还存在残留的频率偏差。如果不能消除偏差,接收机的解调性能将受到该偏差的严重影响,最终导致系统的可靠性降低。因此完成频偏估计和补偿是必要的。
本项目中前导序列中的频偏估计方案如下:

图 2 10用于频偏估计的长度为3840个符号的前导序列
对于本项目来说,帧同步过后剩余3840个符号,其中符号由完美序列组成,完美序列每16个符号为一组,所以共有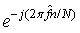 段,每一段都可以计算一个相关值,然后将240个相关值补零后做4096点FFT,其频率分辨率为
段,每一段都可以计算一个相关值,然后将240个相关值补零后做4096点FFT,其频率分辨率为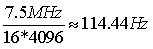 。
。
具体的求频偏估计值算法如下:
位同步和帧同步均已经完成,这里采用基于FFT进行最大似然频偏估计。对于接收到的前导序列,与本地存储的序列进行相关计算,得到240个相关值,在这些相关值后面补3856个零,然后做4096点FFT,对FFT得到的4096个数据取模值,并搜索其最大值位置,则可根据最大值出现的位置计算频偏的粗估计值,然后再基于二次函数拟合的方法进一步估计更精细的频偏。采用的算法如下:
将频率偏移值表示为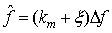 ,其中
,其中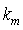 表示FFT幅值最大处对应的频率索引值,
表示FFT幅值最大处对应的频率索引值,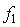 表示真实信号频率与FFT幅值最大点对应索引的偏差,
表示真实信号频率与FFT幅值最大点对应索引的偏差,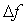 ,
,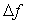 是FFT离散频率间隔(即频率分辨率
是FFT离散频率间隔(即频率分辨率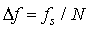 )。
)。
基于FFT插值的频移估计方法主要分为粗估计和细估计两个步骤。粗估计就是搜索FFT结果幅值最大点,得到其索引值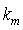 。细估计就是利用插值的方法得到真实频率偏移值与
。细估计就是利用插值的方法得到真实频率偏移值与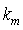 对应频率之间的偏差,即估计
对应频率之间的偏差,即估计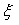 。插值的方法有很多,其中采用最多的就是二次插值方法。二次插值方法描述如下:
。插值的方法有很多,其中采用最多的就是二次插值方法。二次插值方法描述如下:
近似认为信号频域幅度值是一个二次函数,目的是找出这个函数的最大值,而三个点可以确定一个二次函数。先找到相关值FFT结果幅度最大点,再加上其左右各一个点,就可以进行二次插值了。公式推导如下:
假设FFT幅度最大点的坐标为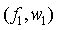 ,左右两点分别为
,左右两点分别为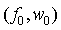 ,
,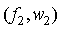 ,其中横坐标表示对应频率值,纵坐标表示FFT结果的幅值。那么根据三点构造二次函数表达式为:
,其中横坐标表示对应频率值,纵坐标表示FFT结果的幅值。那么根据三点构造二次函数表达式为:
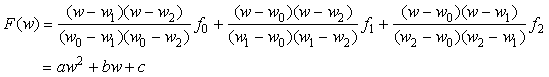
求得:
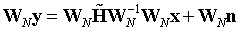
峰值频点横坐标为: 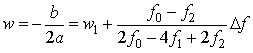
其中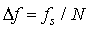 ,最终
,最终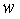 就是估计出来的频率偏移值。
就是估计出来的频率偏移值。

图 2 11频偏估计框图
对于跳频抗干扰算法方案中,由于是同源晶振控制生成的,所以不同频率下的频偏是成比例的。设跳频的频率从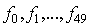 ,在
,在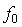 频点下的频偏为
频点下的频偏为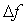 ,则在
,则在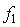 频点下的频偏为
频点下的频偏为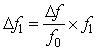 ,则不同频点下的频偏的一般公式为
,则不同频点下的频偏的一般公式为
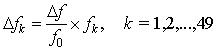 。
。
频偏补偿方案
由上述分析我们可知,计算出频偏估计值后需要对各个子帧的数据进行频偏补偿,这就需要控制直接数字式频率合成器(DDS)在频偏估计后实现频偏补偿。想要补偿频偏,需要在信号上乘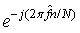 ,而
,而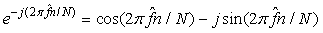 ,正余弦相应的频率可以由DDS产生。
,正余弦相应的频率可以由DDS产生。
在FPGA中DDS核的系统时钟为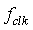 ,输出频率为
,输出频率为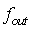 ,则输出频率为
,则输出频率为
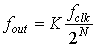
其中,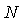 为相位累加器位数,
为相位累加器位数,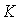 为频率控制字
为频率控制字
频率分辨率,即频率变化的间隔
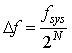
频率控制字即相位增量,其公式为
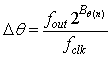
其中,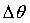 为相位增量,即频率控制字,
为相位增量,即频率控制字,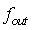 为想要输出的频率,
为想要输出的频率,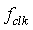 为输入IP的时钟,也是信号的采样时钟,
为输入IP的时钟,也是信号的采样时钟,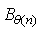 为频率精度的位数,其计算公式如下,取位都为进位。以产生时钟
为频率精度的位数,其计算公式如下,取位都为进位。以产生时钟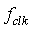 为100MHz,频率精度
为100MHz,频率精度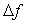 为1Hz计算
为1Hz计算
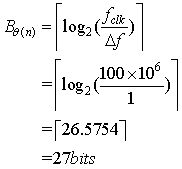
由DDS产生相应相位的sin和cos,与原始数据进行复数乘法即可完成频偏补偿。

图 2 12频偏补偿示意图
对不同的跳频频率点,按上节所述方法计算得到的相应的频偏值。
估计与噪声方差估计方案
信道估计整体流程如图所示。前一阶段的模块将接收信号中的导频部分提取出来并送入去CP、FFT变换模块,信道估计模块接收256个符号长度的导频部分的FFT变换结果,将导频处的点依次送入导频处信道估计计算模块,将其他点的值送入噪声方差计算模块。前者与存储在RAM里的原始导频序列的频域变换值进行运算,得到导频点处的信道估计值,再利用线性插值算法得到每个数据符号的信道估计值,送入频域均衡与解调模块;后者进行噪声方差的计算,将噪声方差估计值传入后级模块。
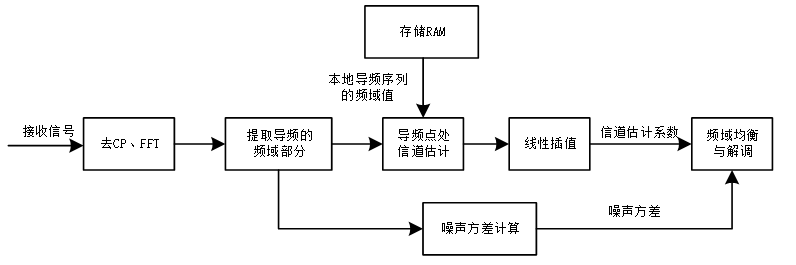
导频由64位Zadoff-Chu序列重复4次得到。Zadoff-Chu序列的数学描述如下式所示:
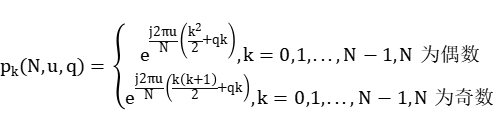
公式中,N表示的是序列的长度,q可以为任意整数,u表示原始序列组数,是与N互质的正整数。q和u取值不同,将得到不同的ZC序列。
Zadoff-Chu序列本身具有良好的自相关性、互相关性、对称性和横幅特性。其中,良好的自相关性意味着对于任意ZC序列与其循环移位m(m≠0)位后的序列互不相关;对称性可以降低生成序列的复杂度;恒幅特性有利于接收端实现信道估计。任意Zadoff-Chu序列经过FFT/IFFT变换后的序列仍为Zadoff-Chu序列,具有Zadoff-Chu序列的所有性质。
选取u=9,q=1,N=64的Zadoff-Chu序列,将其重复4次即得256个符号的导频序列,对该序列进行FFT变换,并对变换结果进行映射。将1映射到1023,将序列进行定点量化为I、Q各11比特数,得到的coe文件。
针对该导频结构,导频点上的信道估计结果很容易得到。将接收的导频点处的FFT变换结果Y与上述文件中的原始ZC序列的频域映射值X相除,即这些点上的频域信道估计值为:
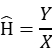
为了提高信道估计系数的精度,利用线性插值算法得到频域上512个点的信道估计值。线性插值是根据信号中两个相邻导频点处的信道相响应之间的线性关系来估计这段数据点上的信道系数的插值方法。线性插值只使用两个相邻的导频点对这段数据进行信道估计,具有易于实现、计算快速的优点。线性插值实现过程如下:
两个相邻导频估计值记作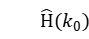 、
、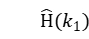 ,设数据点
,设数据点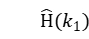 位于区间
位于区间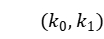 ,则该点的信道估计可表示为:
,则该点的信道估计可表示为:
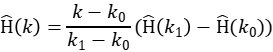
由于除了64个点以外的其他频率点都没有发送信号,接收信号转换到频域在这些点所得到的都是噪声,可以利用这些点的值估算出噪声方差。
频域均衡方案
均衡模块根据信道估计的结果执行相应的算法对信号进行补偿。FFT之后我们得到了各个符号的频域样点,信道估计模块我们得到了每个频域点上对应的信道系数,利用这些数据进行频域均衡,最后将均衡后的信号转为时域信号,硬判决直接对符号的正负进行判决得到最后的结果,处理流程图如图:
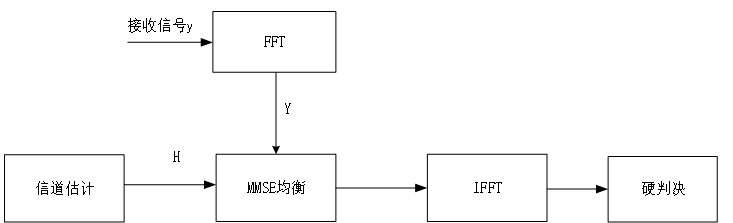
图 2 14频域均衡流程
最小均方误差算法中构造损失函数:
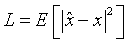
假设,x和z是服从均值为0,方差分别为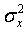 ,
,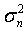 的高斯分布,则MMSE估计为:
的高斯分布,则MMSE估计为:
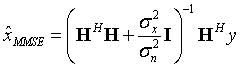
时域上接收信号为发送信号与系统响应的线性卷积,为:
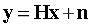
在单载波频域均衡中,由N位符号组成一个数据块,并添加循环前缀,循环前缀的长度大于信道的最大多径时延,以此保证相邻数据块之间没有干扰。在通常情况下,信道在时间上是慢变的,假设连续的两个数据块的传输过程中,信道冲激响应保持不变。由于循环前缀的存在,信道冲激响应矩阵是循环平移矩阵,即: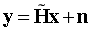 ,其中
,其中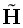 为循环平移矩阵。
为循环平移矩阵。
对接收到的时域信号做FFT变换,得到频域信号。根据信道冲激响应矩阵的循环平移特性,信道频域响应矩阵是对角矩阵。
两边同时做FFT:
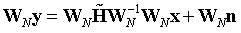
其中,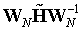 ,
,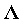 是对角矩阵,其中
是对角矩阵,其中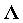 的对角线元素为:
的对角线元素为:
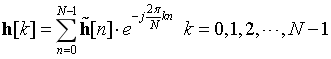
MMSE均衡矢量形式为:
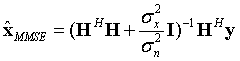
分量形式为:
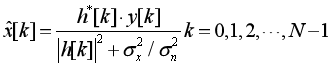
频域MMSE均衡之后的结果再通过IFFT转换到时域,得到时域符号。
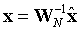
将经过均衡后的时域结果,送到硬判决模块,直接对符号I、Q路数据的正负进行判决,得到解调结果。
matlab代码
clear
clc
CP=25;%CP长度
num_block = 6;%每个子帧中的FDE块数
num_sf = 48; %一帧中的子帧数
rate = 7.5e6;%符号速率
S = 4; % 扩频因子
block=384;%FDE块大小
block_dft=512;
bpc=537; %块+CP
tr_sym = zeros(1,4096+bpc*(num_block+1)*S*num_sf); %一帧中的所有符号,不含GP
err_rate1=zeros(1,9);
s=[];
s1= [1+1j, 1+1j, 1+1j, 1+1j, 1+1j, -1+1j, -1-1j, 1-1j, 1+1j, -1-1j, 1+1j, -1-1j, 1+1j, 1-1j, -1-1j, -1+1j];
for i=1:16
s=[s s1];
end%前16个完美序列,正相位
for i=1:240
s=[s -s1]; %S1重复16次
end %后240个完美序列,反相位
tr_sym(1:4096)=s/sqrt(2);%前导,功率归一化
%以上为生成前导
s2=gen_seq(9);
p=zeros(1,block_dft);
for i=1:block_dft/64
p((i-1)*64+1:i*64) = s2;
end
xx = fft(p);
xx = [xx(509:512),xx(1:508)];%错开本振
p=ifft(xx);%导频生成
b = rcosdesign(0.22, 8,8,'sqrt');%RRC(根升余弦)冲激响应为b
f_pilot = fft(p)/sqrt(block_dft); %导频转换到频域
%rayleighchan = comm.RayleighChannel;
%rayleighchan.SampleRate = 7.5e6;
%rayleighchan.PathGainsOutputPort=1;
%rayleighchan.PathDelays = [0,30e-9,150e-9,310e-9,370e-9,710e-9,1090e-9,1370e-9,2510e-9];
%rayleighchan.PathDelays = [0];%1/7.5e6];%,2/7.5e6,3/7.5e6,4/7.5e6];%,5/7.5e6,6/7.5e6,7/7.5e6,8/7.5e6];
%rayleighchan.AveragePathGains=[0,-1.5,-1.4,-3.6,-0.6,-9.1,-7.0,-12.0,-16.9];
%rayleighchan.MaximumDopplerShift = 50;
snr = 4:1:12;% [4, 5, 6, 7, 8, 9, 10, 11, 12]
err_rate=zeros(size(snr));
nframes = 1000;%传输1000帧
for nsnr = 1:length(snr)%SNR循环,nsnr是索引
sigma = 1/sqrt(2*10^(snr(nsnr)/10));%*sqrt(8);标准差`
total_err=0;
for nfr = 1:nframes %帧循环
bit_fr = randsrc(1,2*num_block*block*num_sf,[1,0]);%生成一个子帧的所有比特(1、0) 因为qpsk所以×2
rbits = zeros(1,2*num_block*block*num_sf);
for nsf = 1:num_sf %子帧循环
bit = bit_fr((nsf-1)*2*num_block*block+1:2*nsf*num_block*block);%每个子帧存储成行向量bit
bit0 = bit(1:2:end-1);%I路:取1 3 5 7bit
bit1 = bit(2:2:end);%Q路: 偶数bit
data = ((1-2.*bit0)+1j*(1-2*bit1))/sqrt(2);%归一化(电平映射从0/1映射到-1/1):QPSK
tx_sframe = zeros(1,(CP+block)*(num_block+1));
tx_sframe(1:CP) = p(block-CP+1:block);%构造导频的CP(取p后几个作为cp)
tx_sframe(CP+1:block_dft+CP) = p;%构造子帧的导频
for i=1:num_block%FDE块数循环
%对每个数据块扩频
% DFT 扩频
fft_block((i-1)*block_dft+1:i*block_dft)= zero_insertion(fft(data((i-1)*block+1:i*block)));
ifft_block((i-1)*block_dft+1:i*block_dft) = ifft(fft_block((i-1)*block_dft+1:i*block_dft),block_dft);
tx_sframe(i*(CP+block_dft)+1:i*(CP+block_dft)+CP) = ifft_block((i-1)*block_dft+(block_dft-CP+1):i*block_dft); %CP是后25个数据
tx_sframe(i*(CP+block_dft)+(CP+1):i*(CP+block_dft)+(CP+block_dft)) = ifft_block((i-1)*block_dft+1:i*block_dft);
end%一个子帧的数据
tr_sym(4097+(nsf-1)*bpc*(num_block+1):4096+nsf*bpc*(num_block+1)) = tx_sframe;
end
% 脉冲成型(A->D)
tr_sample = upfirdn(tr_sym, b, 8);%8倍过采样后过根升余弦滚降
tr_head = [zeros(1,100),tr_sample]; %前面加上GP
%[rx_frame,pathgains] = rayleighchan(tx_frame.');
%h=[0.8, 0, 0, 0.4, 0.4472];
h=1;
%load tx_frame.mat
rx_frame = conv(tr_head,h); %理想信道卷积
%rx_frame = rx_frame.'+randn(size(rx_frame.'))*sigma+1j*randn(size(rx_frame.'))*sigma;
rx_frame = rx_frame.'+randn(size(rx_frame.'))*sigma+1j*randn(size(rx_frame.'))*sigma;
%AWGN加噪声
%%%%%%%%%%%%%%%%%Receiver%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rx_rrc = conv(rx_frame,b);%根升余弦滚降
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%Synchronization%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rx_frame0 = (rx_rrc(1:8:end)).';
rx_frame4 = (rx_rrc(5:8:end)).';
window0=zeros(1,14);
window4=zeros(1,14);
for ii = 1:14 %求十四次相关值
corr0 = conj(s1)*(rx_frame0(ii:ii+15)).';
window0(ii) = abs(real(corr0))+ abs(imag(corr0));
corr4 = conj(s1)*(rx_frame4(ii:ii+15)).';
window4(ii) = abs(real(corr4))+ abs(imag(corr4));
end
bit_syn_ok = 0;
flag0 = 0;
flag4 = 0;
ii = ii+1; %求第十五次相关系数的I路和Q路的绝对值和(相关值)
%%%%%%%%%位同步%%%并行相关%%%%%%%%%%%%%%%%%%%%%%%%%%%
while(~bit_syn_ok)%%对连续的4个周期继续进行匹配滤波??
corr0 = conj(s1)*(rx_frame0(ii:ii+15)).';
abscorr0 = abs(real(corr0))+ abs(imag(corr0));
sumw0 = sum(window0);
if(abscorr0>=0.75*sumw0)%门限值是0.75
bit_syn_ok = 1;
syn_pos = ii;
flag0 = 1;
break;
else
window0=[window0(2:14),abscorr0];
%ii = ii+1;
end
corr4 = conj(s1)*(rx_frame4(ii:ii+15)).';
abscorr4 = abs(real(corr4))+ abs(real(corr4));
sumw4 = sum(window4);
if(abscorr4>=0.75*sumw4)
bit_syn_ok = 1;
syn_pos = ii;
flag4 = 1;
break;
else
window4=[window4(2:14),abscorr4];
end
ii = ii+1;
end
%%%%%%%%% 最佳样值选择
if(flag0)
cor1 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+14)*8+7:8:(ii+77)*8+7));%ii=15
cor2 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+14)*8+8:8:(ii+77)*8+8));
cor3 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+1:8:(ii+78)*8+1));
cor4 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+2:8:(ii+78)*8+2));
cor5 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+3:8:(ii+78)*8+3));
cor6 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+4:8:(ii+78)*8+4));
cor7 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+5:8:(ii+78)*8+5));
cor8 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+6:8:(ii+78)*8+6));
abscor = [abs(real(cor1))+abs(imag(cor1)),abs(real(cor2))+abs(imag(cor2)),abs(real(cor3))+abs(imag(cor3)), ...
abs(real(cor4))+abs(imag(cor4)),abs(real(cor5))+abs(imag(cor5)),abs(real(cor6))+abs(imag(cor6)),...
abs(real(cor7))+abs(imag(cor7)),abs(real(cor8))+abs(imag(cor8))];
[maxabs,pos] = max(abscor);
position = (ii+79)*8+pos-1;
else
cor1 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+3:8:(ii+78)*8+3));
cor2 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+4:8:(ii+78)*8+4));
cor3 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+5:8:(ii+78)*8+5));
cor4 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+6:8:(ii+78)*8+6));
cor5 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+7:8:(ii+78)*8+7));
cor6 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+15)*8+8:8:(ii+78)*8+8));
cor7 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+16)*8+1:8:(ii+79)*8+1));
cor8 = [conj(s1), conj(s1), conj(s1), conj(s1)]*(rx_rrc((ii+16)*8+2:8:(ii+79)*8+2));
abscor = [abs(real(cor1))+abs(imag(cor1)),abs(real(cor2))+abs(imag(cor2)),abs(real(cor3))+abs(imag(cor3)), ...
abs(real(cor4))+abs(imag(cor4)),abs(real(cor5))+abs(imag(cor5)),abs(real(cor6))+abs(imag(cor6)),...
abs(real(cor7))+abs(imag(cor7)),abs(real(cor8))+abs(imag(cor8))];
[maxabs,pos] = max(abscor);
position = (ii+79)*8+pos+2;
end
%position
pre_cor = conj(s1)*rx_rrc(position:8:position+15*8);
frame_syn = 0;
curr = position;
while(frame_syn==0)
curr = curr+16*8;
curr_cor = conj(s1)*rx_rrc(curr:8:curr+15*8);
xc = pre_cor*conj(curr_cor);
if(real(xc)<0)
frame_syn = 1;
else
pre_cor = curr_cor;
end
end
data_for_fre_offsetEst = rx_rrc(curr:8:curr+3839*8);%用于频偏估计
data_for_fre_offsetCmp = rx_rrc(curr+3840*8:8:end);%用于频偏补偿
%%%%%%%%%%%%%%%%%%%%频偏估计%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 用于频偏估计的长度为3840个符号的前导序列
corr_res = zeros(1,240);
%与本地存储的序列进行相关计算,得到240个相关值,在这些相关值后面补3856个零
for i=1:16:3840
corr_res((i+15)/16)=conj(-s1)*data_for_fre_offsetEst(i:i+15);
end
%得到的corr_res做4096点FFT(基于FFT进行最大似然频偏估计)
fft_value = fft(corr_res,4096);
%对fft_value求模平方
fft_value=real(fft_value).*real(fft_value)+imag(fft_value).*imag(fft_value);
%找最大值,记录最大值所在的位置索引loca_tmp
[fft_value1,loca_tmp]=max(fft_value);
%进行二次插值
%求最大值左边一个位置的值
fft_value0=fft_value(mod((loca_tmp-2),4096)+1);
%求最大值右边一个位置的值
fft_value2=fft_value(mod(loca_tmp,4096)+1);
%根据公式拟合出二次函数,并找到最大值
% 频率偏移值
fre_off_est=((loca_tmp-1)+(fft_value0-fft_value2)/(2*fft_value0-4*fft_value1+2*fft_value2))*(rate/16/4096);
%%%%%%%%%%%%%%%%%%%频偏补偿%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
t = 0:1/rate:(length(data_for_fre_offsetCmp)-1)/rate;
data_for_EstEqu = data_for_fre_offsetCmp.'.*exp(-1j*2*pi*fre_off_est.*t);
%%%%%%%%%%%%%%%%%%提取信息%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for nsf = 1:num_sf
rx_frame = data_for_EstEqu((nsf-1)*3759+1:nsf*3759);
pilot_r = rx_frame(CP+1:CP+block_dft);
data_r = zeros(1,num_block*block_dft);
f_data_r = zeros(1,num_block*block_dft);
for i=1:num_block
data_r((i-1)*block_dft+1:i*block_dft) = rx_frame(i*(CP+block_dft)+CP+1:i*(CP+block_dft)+(CP+block_dft));
f_data_r((i-1)*block_dft+1:i*block_dft) = fft(data_r((i-1)*block_dft+1:i*block_dft))/sqrt(block_dft);
end
%对子帧的导频做fft,进行信道估计
f_pilot_r = fft(pilot_r)/sqrt(block_dft);
r_for_sigma=f_pilot_r(1:4);
for i=1:63
r_for_sigma=[r_for_sigma,f_pilot_r((i-1)*block_dft/64+6:(i-1)*block_dft/64+12)];
end
r_for_sigma=[r_for_sigma,f_pilot_r(510:512)];
sigma_est = sqrt(mean(abs(r_for_sigma).^2)/2);
pace=block_dft/64;
h_est = f_pilot_r(5:pace:end)./f_pilot(5:pace:end);
h_est_interp = zeros(1,block_dft);
for i=2:64
delta = (h_est(i)-h_est(i-1))/8;
for k=1:block_dft/64
h_est_interp((i-2)*8+k+4) = h_est(i-1)+(k-1)*delta;
end
end
delta = (h_est(1)-h_est(64))/8;
for k=509:512
h_est_interp(k) = h_est(64)+(k-509)*delta;
end
for k=1:4
h_est_interp(k) = h_est(64)+(k+3)*delta;
end
comp = zeros(1,num_block*block_dft);
r_cons = zeros(1,num_block*block);
for i=1:num_block
for k=1:block_dft
comp((i-1)*block_dft+k) = f_data_r((i-1)*block_dft+k)*conj(h_est_interp(k))/(h_est_interp(k)*conj(h_est_interp(k))+sigma_est*sigma_est);
end
f_data_remov((i-1)*block+1:i*block) = zero_removal(comp((i-1)*block_dft+1:i*block_dft));
r_cons((i-1)*block+1:i*block) = ifft(f_data_remov((i-1)*block+1:i*block))*sqrt(block);
end
rsyms = reshape([real(r_cons);imag(r_cons)],1,2*num_block*block);
rbits((nsf-1)*2*num_block*block+1:nsf*2*num_block*block) = rsyms<0;
%小于0 为1
end
tbits = bit_fr==1;
[err_count,err_rate]=biterr(tbits,rbits);
total_err = total_err+err_count;
end
disp('准备打印图片');
err_rate1(nsnr)=total_err/(2*num_block*block*num_sf*nframes);
end
figure
semilogy(snr,err_rate1);
%rx_frame = tx_frame;
% end
% err_rate(nsnr)=total_err/(2*num_block*block*nframes);
% end



