ysyx预学习记录--pa1
写下此篇以记录pa1的完成过程:缺乏一些知识和对数据结构、c语言基础不扎实的情况下,不断的debug和理解框架代码查阅资料中完成”简答”的pa1。充分认识自己本科知识的不扎实 😑,前半部分是讲义的知识点以及我的小更改,后半部分是代码和思路实现,由于本博客只是我自己学习记录从未发布,所以不存在分享代码的情况
试运行游戏
make ARCH=native run mainargs=mario
编译有点慢?
make程序默认使用单线程来顺序地编译所有文件
需要通过lscpu命令来查询你的系统中有多少个CPU. 然后在运行make的时候添加一个-j?的参数, 其中?为你查询到的CPU数量

为了查看编译加速的效果, 你可以在编译的命令前面添加time命令, 它将会对紧跟在其后的命令的执行时间进行统计, 你只需要关注total一栏的时间即可. 你可以通过make clean清除所有的编译结果, 然后重新编译并统计时间, 对比单线程编译和多线程编译的编译时间; 你也可以尝试不同的线程数量进行编译, 并对比加速比.
ccache
如果你通过man阅读ccache的手册, 你会发现ccache是一个compiler cache. cache是计算机领域中的一个术语, 你将会在后续的ICS课程中学习相关的内容.
为了使用ccache, 你还需要进行一些配置的工作. 首先运行如下命令来查看一个命令的所在路径:
which gcc它默认会输出/usr/bin/gcc, 表示当你执行gcc命令时, 实际执行的是/usr/bin/gcc. 作为一个RTFM的练习, 接下来你需要阅读man ccache中的内容, 并根据手册的说明, 在.bashrc文件中对某个环境变量进行正确的设置. 如果你的设置正确且生效, 重新运行which gcc, 你将会看到输出变成了/usr/lib/ccache/gcc.
- 在
.bashrc文件中添加环境变量的设置。假设您希望将gcc命令指向/usr/lib/ccache/gcc,您可以添加以下行:
export PATH="/usr/lib/ccache:$PATH"- 让修改生效。运行以下命令以使更改生效:
source ~/.bashrcsource ~/.bashrc是一个Bash shell命令,用于在当前的Bash会话中加载(或重新加载).bashrc文件的内容。这个命令会读取并执行.bashrc文件中的所有命令,从而使文件中定义的别名、环境变量、函数和其他配置生效。
现在就可以来体验ccache的效果了. 首先先清除编译结果, 然后重新编译并统计时间. 你会发现这次编译时间反而比之前要更长一些, 这是因为除了需要开展正常的编译工作之外, ccache还需要花时间把目标文件存起来. 接下来再次清除编辑结果, 重新编译并统计时间, 你会发现第二次编译的速度有了非常明显的提升! 这说明ccache确实跳过了完全重复的编译过程, 发挥了加速的作用. 如果和多线程编译共同使用, 编译速度还能进一步加快!
为NEMU编译时添加GDB调试信息
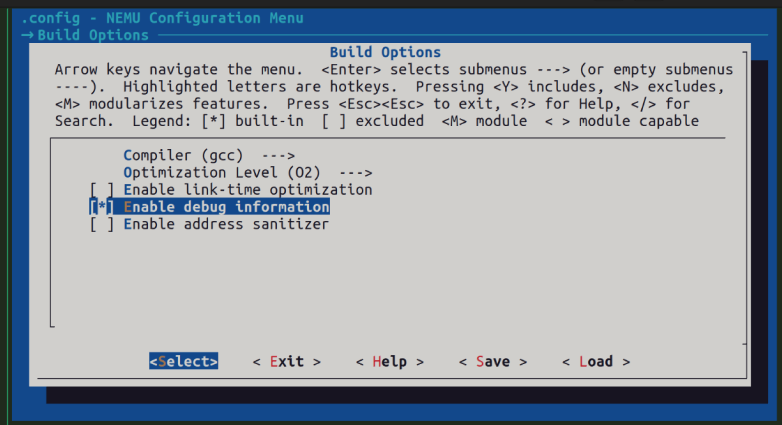
menuconfig已经为大家准备好相应选项了, 你只需要打开它:
Build Options
[*] Enable debug information然后清除编译结果并重新编译即可. 尝试阅读相关代码, 理解开启上述menuconfig选项后会导致编译NEMU时的选项产生什么变化.
make menuconfig
运行
make run框架代码
NEMU主要由4个模块构成: monitor, CPU, memory, 设备. 我们已经在上一小节简单介绍了CPU和memory的功能, 设备会在PA2中介绍, 目前不必关心.
Monitor(监视器)模块是为了方便地监控客户计算机的运行状态而引入的. 它除了负责与GNU/Linux进行交互(例如读入客户程序)之外, 还带有调试器的功能, 为NEMU的调试提供了方便的途径. 从概念上来说, monitor并不属于一个计算机的必要组成部分, 但对NEMU来说, 它是必要的基础设施. 如果缺少monitor模块, 对NEMU的调试将会变得十分困难.
配置系统kconfig
在一个有一定规模的项目中, 可配置选项的数量可能会非常多, 而且配置选项之间可能会存在关联, 比如打开配置选项A之后, 配置选项B就必须是某个值. 直接让开发者去管理这些配置选项是很容易出错的, 比如修改选项A之后, 可能会忘记修改和选项A有关联的选项B. 配置系统的出现则是为了解决这个问题.
NEMU中的配置系统位于nemu/tools/kconfig, 它来源于GNU/Linux项目中的kconfig, 我们进行了少量简化. kconfig定义了一套简单的语言, 开发者可以使用这套语言来编写”配置描述文件”. 在”配置描述文件”中, 开发者可以描述:
- 配置选项的属性, 包括类型, 默认值等
- 不同配置选项之间的关系
- 配置选项的层次关系
在NEMU项目中, “配置描述文件”的文件名都为Kconfig, 如nemu/Kconfig. 当你键入make menuconfig的时候, 背后其实发生了如下事件:
检查
nemu/tools/kconfig/build/mconf程序是否存在, 若不存在, 则编译并生成mconf检查
nemu/tools/kconfig/build/conf程序是否存在, 若不存在, 则编译并生成conf运行命令
mconf nemu/Kconfig, 此时mconf将会解析nemu/Kconfig中的描述, 以菜单树的形式展示各种配置选项, 供开发者进行选择退出菜单时,
mconf会把开发者选择的结果记录到nemu/.config文件中运行命令
conf --syncconfig nemu/Kconfig, 此时
conf将会解析
nemu/Kconfig中的描述, 并读取选择结果
nemu/.config, 结合两者来生成如下文件:
- 可以被包含到C代码中的宏定义(
nemu/include/generated/autoconf.h), 这些宏的名称都是形如CONFIG_xxx的形式 - 可以被包含到Makefile中的变量定义(
nemu/include/config/auto.conf) - 可以被包含到Makefile中的, 和”配置描述文件”相关的依赖规则(
nemu/include/config/auto.conf.cmd), 为了阅读代码, 我们可以不必关心它 - 通过时间戳来维护配置选项变化的目录树
nemu/include/config/, 它会配合另一个工具nemu/tools/fixdep来使用, 用于在更新配置选项后节省不必要的文件编译, 为了阅读代码, 我们可以不必关心它
- 可以被包含到C代码中的宏定义(
所以, 目前我们只需要关心配置系统生成的如下文件:
nemu/include/generated/autoconf.h, 阅读C代码时使用nemu/include/config/auto.conf, 阅读Makefile时使用
项目构建和Makefile
NEMU的Makefile会稍微复杂一些, 它具备如下功能:
#与配置系统进行关联
通过包含nemu/include/config/auto.conf, 与kconfig生成的变量进行关联. 因此在通过menuconfig更新配置选项后, Makefile的行为可能也会有所变化.
#文件列表(filelist)
通过文件列表(filelist)决定最终参与编译的源文件. 在nemu/src及其子目录下存在一些名为filelist.mk的文件, 它们会根据menuconfig的配置对如下4个变量进行维护:
SRCS-y- 参与编译的源文件的候选集合SRCS-BLACKLIST-y- 不参与编译的源文件的黑名单集合DIRS-y- 参与编译的目录集合, 该目录下的所有文件都会被加入到SRCS-y中DIRS-BLACKLIST-y- 不参与编译的目录集合, 该目录下的所有文件都会被加入到SRCS-BLACKLIST-y中
Makefile会包含项目中的所有filelist.mk文件, 对上述4个变量的追加定义进行汇总, 最终会过滤出在SRCS-y中但不在SRCS-BLACKLIST-y中的源文件, 来作为最终参与编译的源文件的集合.
Makefile的编译规则在nemu/scripts/build.mk中定义:
$(OBJ_DIR)/%.o: %.c
@echo + CC $<
@mkdir -p $(dir $@)
@$(CC) $(CFLAGS) -c -o $@ $<
$(call call_fixdep, $(@:.o=.d), $@)其中关于$@和$<等符号的含义, 可以RTFM进行了解. call_fixdep的调用用于生成更合理的依赖关系, 目前我们主要关注编译的命令, 因此可以先忽略call_fixdep.
我们已经在上文提到过, kconfig会根据配置选项的结果在 nemu/include/generated/autoconf.h中定义一些形如CONFIG_xxx的宏, 我们可以在C代码中通过条件编译的功能对这些宏进行测试, 来判断是否编译某些代码. 例如, 当CONFIG_DEVICE这个宏没有定义时, 设备相关的代码就无需进行编译.
为了编写更紧凑的代码, 我们在nemu/include/macro.h中定义了一些专门用来对宏进行测试的宏. 例如IFDEF(CONFIG_DEVICE, init_device());表示, 如果定义了CONFIG_DEVICE, 才会调用init_device()函数; 而MUXDEF(CONFIG_TRACE, "ON", "OFF")则表示, 如果定义了CONFIG_TRACE, 则预处理结果为"ON"("OFF"在预处理后会消失), 否则预处理结果为"OFF".
第一项工作就是将一个内置的客户程序读入到内存中. 为了理解这项工作, 我们还需要理清三个问题:
- 客户程序是什么? 我们知道, 程序是由指令构成的, 而不同ISA的指令也各不相同(想象一下用不同的语言来表达”你好”的意思), 因而程序本身肯定是ISA相关的. 因此, 我们把内置客户程序放在
nemu/src/isa/$ISA/init.c中. 内置客户程序的行为非常简单, 它只包含少数几条指令, 甚至算不上在做一些有意义的事情. - 内存是什么? 我们可以把内存看作一段连续的存储空间, 而内存又是字节编址的(即一个内存位置存放一个字节的数据), 在C语言中我们就很自然地使用一个
uint8_t类型的数组来对内存进行模拟. NEMU默认为客户计算机提供128MB的物理内存(见nemu/src/memory/paddr.c中定义的pmem), - 需要将客户程序读入到内存的什么位置? 为了让客户计算机的CPU可以执行客户程序, 因此我们需要一种方式让客户计算机的CPU知道客户程序的位置. 我们采取一种最简单的方式: 约定. 具体地, 我们让monitor直接把客户程序读入到一个固定的内存位置
RESET_VECTOR.RESET_VECTOR的值在nemu/include/memory/paddr.h中定义.
优美地退出
为了测试大家是否已经理解框架代码, 我们给大家设置一个练习: 如果在运行NEMU之后直接键入
q退出, 你会发现终端输出了一些错误信息. 请分析这个错误信息是什么原因造成的, 然后尝试在NEMU中修复它.
更改sdb.c中
static int cmd_q(char *args) {
nemu_state.state = NEMU_QUIT; //不确定这么改好不好
return -1;makefile真牛B
Simple Debugger, sdb
总体要求:
| 命令 | 格式 | 使用举例 | 说明 |
|---|---|---|---|
| 帮助(1) | help |
help |
打印命令的帮助信息 |
| 继续运行(1) | c |
c |
继续运行被暂停的程序 |
| 退出(1) | q |
q |
退出NEMU |
| 单步执行 | si [N] |
si 10 |
让程序单步执行N条指令后暂停执行, 当N没有给出时, 缺省为1 |
| 打印程序状态 | info SUBCMD |
info r info w |
打印寄存器状态 打印监视点信息 |
| 扫描内存(2) | x N EXPR |
x 10 $esp |
求出表达式EXPR的值, 将结果作为起始内存 地址, 以十六进制形式输出连续的N个4字节 |
| 表达式求值 | p EXPR |
p $eax + 1 |
求出表达式EXPR的值, EXPR支持的 运算请见调试中的表达式求值小节 |
| 设置监视点 | w EXPR |
w *0x2000 |
当表达式EXPR的值发生变化时, 暂停程序执行 |
| 删除监视点 | d N |
d 2 |
删除序号为N的监视点 |
单步执行 si [N]
主要理解ysyx框架的代码,理解cpu excute的机制:
static int cmd_si(char *args) {
int n=1;
// printf("%s\n", args);
if(args != NULL){
sscanf(args, "%d", &n);
}
printf("move %dword(s)\n", n);
cpu_exec(n);
return 0;
}观察代码理解 cpu_exec(n)的意思,然后从命令行输入中提取出n的值,即可完成
info SUBCMD
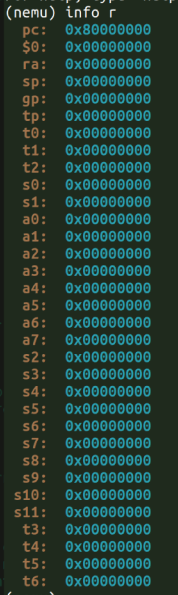
info r
打印pc和所有其他寄存器:
实现思路
ysyx在reg.c中预留好了接口,稍作修改即可:
void isa_reg_display() {
printf("\033[0m\033[1;33m %3s:\033[0m \033[0m\033[1;36m 0x%08x\033[0m\n", "pc", cpu.pc);
for (int i = 0; i < 32; i++) {
printf("\033[0m\033[1;33m %3s:\033[0m \033[0m\033[1;36m 0x%08x\033[0m\n", regs[i], gpr(i));
}
}info w
打印监视点状态,做完监视点后会预留一个 监视点信息打印的接口inf
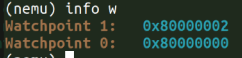
实现思路
见后面监视点
扫描内存 x N EXPR
扫描内存的实现也不难, 对命令进行解析之后, 先求出表达式的值.
x 10 0x80000000解析出待扫描内存的起始地址之后, 就可以使用循环将指定长度的内存数据通过十六进制打印出来. 如果你不知道要怎么输出, 同样的, 你可以参考GDB中的输出. 问题是, 我们要如何访问客户计算机的内存数据呢?
RTFSC中:
内存通过在
nemu/src/memory/paddr.c中定义的大数组pmem来模拟. 在客户程序运行的过程中, 总是使用vaddr_read()和vaddr_write()(在nemu/src/memory/vaddr.c中定义)来访问模拟的内存. vaddr, paddr分别代表虚拟地址和物理地址. 这些概念在将来才会用到, 目前不必深究, 但从现在开始保持接口的一致性可以在将来避免一些不必要的麻烦.static int cmd_x(char *args) { //扫描内存 int N=1; char* EXPR = (char*)malloc(65535); bool success = true; int result = sscanf(args, "%d %s", &N, EXPR); word_t addr = expr(EXPR, &success); if (result != 2||N==0) { printf("Invalid input format. Expected 'x N EXPR'.\n"); return 1; }else { int j=0; for(int i=0; i<N; i++){ if(j==0){ printf("\033[32m 0x%08x : \033[0m ",addr); j=0; } printf("0x%08x ", paddr_read(addr,4)) ; j++; if(j==4){ printf("\n"); j=0; } addr += 4; } printf("\n"); } return 0; }sscanf 返回值是成功匹配并提取的参数个数
完成这个的前提是表达式求值
实现思路
关键要理解内存的模型,理清楚word byte 等等关系后再计算偏移量

这期间遇到一些小问题
在我输入0x80000001后,发现内存并不是直接向后移动一个字节,查阅riscV 后发现是大小端的问题,但是具体原因还没完全理解,等再补充一些内存的知识后再来解释。
表达式求值 p EXPR
这个是pa1里的重难点。
词法分析
第一步首先学习正则表达式,把需要的子串提取出来
{"\\$[0-9a-z]+", TK_REG}, // reg
{"0[xX][0-9a-fA-F]+", TK_HEXNUM}, // 16进制
{" +", TK_NOTYPE}, // spaces 匹配多个空格
{"\\*", '*'}, // multiply
{"\\/", '/'}, // divide
{"\\(", '('}, // left bracket
{"\\)", ')'}, // right bracket
{"[0-9]+", TK_NUM}, // decimal
{"\\-", '-'}, // minus
{"\\+", '+'}, // plus
{"==", TK_EQ}, // doubleequal
{"!=", TK_NOTEQ}, // not equal
{"<=", TK_LESSEQ}, // less equal
{">=", TK_GREATEQ}, // greater equal
{"<", '<'}, // less
{">", '>'}, // greater
{"&&", TK_AND}, // and
{"\\|\\|", TK_OR}, // or
{"!", '!'} // not需要注意的是reg类型我并没有在一开始做判断输入是否合法(是否RISC V的reg名称)而是在reg求值的函数中判断。
另外指针类型并未出现在这个表中,是因为在后续区分*是乘还是指针时再进行判断。
token结构体如下
typedef struct token {
int type;
char str[32];
} Token;其中type成员用于记录token的类型. 大部分token只要记录类型就可以了, 例如+, -, *, /, 但这对于有些token类型是不够的: 如果我们只记录了一个十进制整数token的类型, 在进行求值的时候我们还是不知道这个十进制整数是多少. 这时我们应该将token相应的子串也记录下来, str成员就是用来做这件事情的
实现思路
具体解析过程是在make_token函数中进行
static bool make_token(char *e)
{
int position = 0; // 当前处理到的位置
int i;
regmatch_t pmatch;
nr_token = 0;
while (e[position] != '\0')
{
/* Try all rules one by one. */
for (i = 0; i < NR_REGEX; i++)
{
if (regexec(&re[i], e + position, 1, &pmatch, 0) == 0 && pmatch.rm_so == 0)
{
char *substr_start = e + position;
int substr_len = pmatch.rm_eo;
Log("match rules[%d] = \"%s\" at position %d with len %d: %.*s",
i, rules[i].regex, position, substr_len, substr_len, substr_start);
position += substr_len;
/* TODO: Now a new token is recognized with rules[i]. Add codes
* to record the token in the array `tokens'. For certain types
* of tokens, some extra actions should be performed.
*/
switch (rules[i].token_type)
{
case TK_NOTYPE:
break;
case TK_NUM:
{
tokens[nr_token].type = TK_NUM;
strncpy(tokens[nr_token].str, substr_start, substr_len);
tokens[nr_token].str[substr_len] = '\0';
nr_token++;
break;
}
case '+':
{
tokens[nr_token].type = '+';
nr_token++;
break;
}
case '-':
{
tokens[nr_token].type = '-';
nr_token++;
break;
}
case '*':
{
if (nr_token == 0 || (tokens[nr_token - 1].type != TK_NUM && tokens[nr_token - 1].type != ')'&& tokens[nr_token - 1].type != TK_HEXNUM&& tokens[nr_token - 1].type != TK_REG))
{
tokens[nr_token].type = TK_DEREF; // 判断是不是指针:GDB里 1**1也能识别为指针
}
else
{
tokens[nr_token].type = '*';
}
nr_token++;
break;
}
case '/':
{
tokens[nr_token].type = '/';
nr_token++;
break;
}
case '(':
{
tokens[nr_token].type = '(';
nr_token++;
break;
}
case ')':
{
tokens[nr_token].type = ')';
nr_token++;
break;
}
case TK_EQ:
{
tokens[nr_token].type = TK_EQ;
nr_token++;
break;
}
case TK_NOTEQ:
{
tokens[nr_token].type = TK_NOTEQ;
nr_token++;
break;
}
case TK_AND:
{
tokens[nr_token].type = TK_AND;
nr_token++;
break;
}
case TK_OR:
{
tokens[nr_token].type = TK_OR;
nr_token++;
break;
}
case TK_REG:
{
tokens[nr_token].type = TK_REG;
strncpy(tokens[nr_token].str, substr_start + 1, substr_len - 1);
tokens[nr_token].str[substr_len] = '\0';
nr_token++;
break;
}
case TK_HEXNUM:
{
tokens[nr_token].type = TK_HEXNUM;
strncpy(tokens[nr_token].str, substr_start, substr_len);
tokens[nr_token].str[substr_len] = '\0';
nr_token++;
break;
}
case TK_GREATEQ:
{
tokens[nr_token].type = TK_GREATEQ;
nr_token++;
break;
}
case TK_LESSEQ:
{
tokens[nr_token].type = TK_LESSEQ;
nr_token++;
break;
}
case '>':
{
tokens[nr_token].type = '>';
nr_token++;
break;
}
case '<':
{
tokens[nr_token].type = '<';
nr_token++;
break;
}
case '!':
{
tokens[nr_token].type = '!';
nr_token++;
break;
}
default:
break;
}
break;//退出for循环
}
if (nr_token == 65536)
{
Assert(0,"Too many tokens!\n");
return false;
}
}
if (i == NR_REGEX)
{
printf("no match at position %d\n%s\n%*.s^\n", position, e, position, "");
return false;
}
}
if ((tokens[0].type != TK_NUM && tokens[0].type != TK_REG && tokens[0].type != '(' && tokens[0].type != TK_HEXNUM && tokens[0].type != TK_DEREF && tokens[0].type != '!') ||
(tokens[nr_token - 1].type != TK_NUM && tokens[nr_token - 1].type != TK_REG && tokens[nr_token - 1].type != TK_HEXNUM && tokens[nr_token - 1].type != ')'))
{
printf("%d\n",tokens[0].type);
printf("Invalid expression!\n");
return false;
}
return true;
}
整体思路是在框架代码遍历字符串的过程中,对每一个字符进行正则匹配,匹配到后,根据type字段写一个switch来判断具体的类型,并对str字段进行赋值。
需要注意的是如下几种情况
TK_NUM:数字类型
记录整个字符串(因为未知长度)
*:判断是指针类型还是乘法
思路是判断前一个tokens是否为数字、寄存器或者’)’
最后需要判断,tokens是否溢出,以及是否有不匹配的情况
另外需要判断是否存在字符串不是表达式的情况
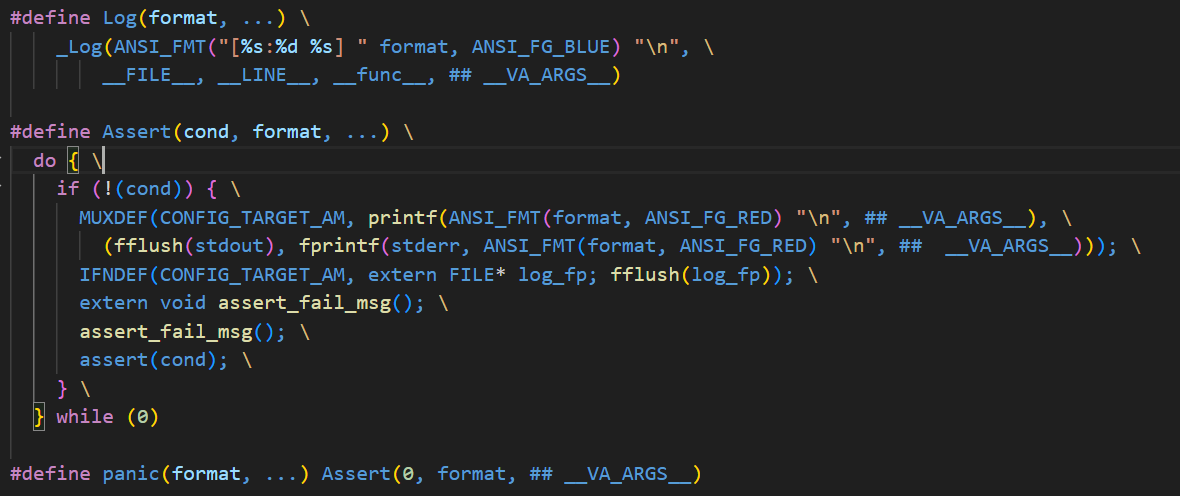
值得注意的是框架在debug.h中定义的调试函数
在讲义的前面也有记录,可以用作错误处理
递归求值
把待求值表达式中的token都成功识别出来之后, 接下来我们就可以进行求值了. 需要注意的是, 我们现在是在对tokens数组进行处理, 为了方便叙述, 我们称它为”token表达式”. 例如待求值表达式
"4 +3*(2- 1)"的token表达式为
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| NUM | '+' | NUM | '*' | '(' | NUM | '-' | NUM | ')' |
| "4" | | "3" | | | "2" | | "1" | |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+根据表达式的归纳定义特性, 我们可以很方便地使用递归来进行求值. 首先我们给出算术表达式的归纳定义:
<expr> ::= <number> # 一个数是表达式
| "(" <expr> ")" # 在表达式两边加个括号也是表达式
| <expr> "+" <expr> # 两个表达式相加也是表达式
| <expr> "-" <expr> # 接下来你全懂了
| <expr> "*" <expr>
| <expr> "/" <expr>归纳定义(Inductive Definition)是一种在数学和计算机科学中常用的定义方式。它通过对基本情况进行定义,并通过一系列规则来扩展或推导出其他情况。归纳定义允许我们用简洁的方式描述一类对象或结构,并展示它们的特定性质和行为。
BNF 使用一组产生式(Production)来描述形式语言的语法规则。每个产生式包含一个非终结符和一个或多个符号序列,表示该非终结符可以通过替换其中的符号序列来生成一个字符串。在 BNF 中,非终结符用尖括号括起来,而终结符则是实际的语言元素。
BNF 中的产生式遵循以下语法形式:
phpCopy code
<非终结符> ::= <符号序列>其中,<非终结符> 表示一个非终结符,::= 表示定义,而 <符号序列> 则是由终结符和非终结符组成的序列。
既然长表达式是由短表达式构成的, 我们就先对短表达式求值, 然后再对长表达式求值. 这种十分自然的解决方案就是分治法open in new window的应用, 就算你没听过这个高大上的名词, 也不难理解这种思路. 而要实现这种解决方案, 递归是你的不二选择.
递归求值思路
word_t eval(int p, int q)
{
if (p > q)
{
// printf("p>q\n");
// printf("check_op = %d\n",deter_main_op(0, nr_token - 1));
// printf("%d\n",nr_token);
// printf("%d %d\n",p,q);
Assert(p <= q, "The expression is not valid!");
return 0;
}
else if (p == q)
{
// printf("p==q\n");
// printf("str = %s\n",tokens[p].str);
bool success = true;
int result = 0;
if (tokens[p].type == TK_NUM)
{
result = atoi(tokens[p].str); // 10进制数字
}
else if (tokens[p].type == TK_REG)
{
int temp = isa_reg_str2val(tokens[p].str, &success); // 寄存器
if(success)
result = temp;
else
Assert(0,"regisiter not exist"); // 寄存器不存在
}
else if (tokens[p].type == TK_HEXNUM)
{
sscanf(tokens[p].str, "%x", &result); // 16进制数字
}
return result;
}
else if (!check_parentheses(p, q))
{
// printf("有括弧\n");
Assert(check_parentheses(p, q) != invalid, "The expression is not surrounded by matched pairs of parentheses.");
// 括弧不匹配直接退出
/* The expression is surrounded by a matched pair of parentheses.
* If that is the case, just throw away the parentheses.
*/
return eval(p + 1, q - 1);
}
else
{
// printf("p<q\n");
int op = deter_main_op(p, q); // the position of 主运算符 in the token expression;
if (tokens[op].type == TK_DEREF)
{
word_t addr = eval(op + 1, q);
return (word_t)vaddr_read(addr, 4);
}
else if (tokens[op].type == '!')
{
return (word_t)!eval(op + 1, q);
}
else
{
word_t val1 = eval(p, op - 1);
// printf("val1 = %u\n",val1);
word_t val2 = eval(op + 1, q);
// printf("val2 = %u\n",val2);
switch (tokens[op].type)
{
case TK_EQ:
return (word_t)val1 == val2;
case TK_GREATEQ:
return (word_t)val1 >= val2;
case TK_LESSEQ:
return (word_t)val1 <= val2;
case '>':
return (word_t)val1 > val2;
case '<':
return (word_t)val1 < val2;
case TK_NOTEQ:
return (word_t)val1 != val2;
case TK_AND:
return (word_t)val1 && val2;
case TK_OR:
return (word_t)val1 || val2;
case '+':
return (word_t)val1 + val2;
case '-':
return (word_t)val1 - val2;
case '*':
return (word_t)val1 * val2;
case '/':
if (val2 == 0)
{
printf("Divide 0!\n");
Assert(0, "Divide 0!");
}
else
return (word_t)val1 / val2;
default:
assert(0);
return 0;
}
}
}
}
这边根据框架代码的递归思路可以很好的理解表达式求值,具体流程如下:
"4 + 3 * ( 2 - 1 )"
/*********************/
case 1:
"+"
/ \
"4" "3 * ( 2 - 1 )"
case 2:
"*"
/ \
"4 + 3" "( 2 - 1 )"
case 3:
"-"
/ \
"4 + 3 * ( 2" "1 )"需要注意的有两点:
- 判断括号匹配时候,不光要判断是否匹配还要找出:匹配但是不满足现在这种情况的形式。这里check_parentheses(p, q)是检查”(4 + 3 * (2 - 1))” 这种形式的括弧匹配,如果存在诸如”(4 + 3 * (2 - 1))” 形式,虽然也是匹配但是不满足情况。
- 找主运算符
括弧匹配的解决思路
int check_parentheses(int p, int q)
{
bool valid_but_imposs_flag = false; // 标记是否为有效但不可能的情况
if (tokens[p].type != '(' || tokens[q].type != ')')
{
// 如果第一个字符不是左括号,或者最后一个字符不是右括号1+(2+3)
valid_but_imposs_flag = true;
}
// 定义一个栈来保存左括号的位置
#define MAX_LEN q - p + 1
int stack[MAX_LEN] __attribute__((unused));
int top = 0; // 栈顶指针
for (int i = p; i <= q; i++)
{
if (tokens[i].type == '(')
{
// 如果遇到左括号,将其位置压入栈中
stack[top++] = i;
// if (pop_flag==true) {
// valid_but_imposs_flag=1;
// }
}
else if (tokens[i].type == ')')
{
// 如果遇到右括号,检查栈是否为空
if (top == 0)
{
// 栈为空,表示右括号没有匹配的左括号,括号不匹配
// pop_flag=true;
return invalid;
}
else
{
// 弹出栈顶元素,与当前右括号匹配
top--;
if (top == 0 && i != q)
{
valid_but_imposs_flag = 1;
}
// pop_flag=true;
}
}
// 其他字符直接跳过
}
if (valid_but_imposs_flag == true)
{
return VALID_IMPOSS;
}
// 遍历结束后,检查栈是否为空
return !(top == 0);
}在传统用栈进行括弧匹配的操作上判断类型
发现()+()该种情况会存在一瞬间的栈空的情况,所以每次遇到“)”时候判断一下栈是否为空(除非是最后一个括弧),为空的就是此种情况。
确定主运算符思路
int deter_main_op(int p, int q)
{
int op = p;
int op_type = 6; // 1: + - 2: * /(主运算符一定在更低优先级位置)
// op_type 为主运算符的优先级
int parentheses = 0;
for (int i = p; i <= q; i++)
{
if (tokens[i].type == TK_NUM)
continue; // 跳过数字
if (tokens[i].type == '(')
{
parentheses++;
}
else if (tokens[i].type == ')')
{
parentheses--;
}
else if (parentheses == 0)
{ //=0时,说明在括弧外层
if (tokens[i].type == TK_OR || tokens[i].type == TK_AND)
{
if (op_type >= 1)
{
op = i;
op_type = 1;
}
}
else if (tokens[i].type == '>' || tokens[i].type == '<' || tokens[i].type == TK_EQ || tokens[i].type == TK_NOTEQ || tokens[i].type == TK_LESSEQ || tokens[i].type == TK_GREATEQ)
{
if (op_type >= 2)
{
op = i;
op_type = 2;
}
}
else if (tokens[i].type == '+' || tokens[i].type == '-')
{
if (op_type >= 3)
{
op = i;
op_type = 3;
}
}
else if (tokens[i].type == '*' || tokens[i].type == '/')
{
if (op_type >= 4)
{
op = i;
op_type = 4;
}
}
else if (tokens[i].type == TK_DEREF || tokens[i].type == '!')
{ // 指针运算优先级最高
if (op_type >= 5)
{
op = i;
op_type = 5;
}
}
}
}
return op;
}这里主要考虑了运算符的优先级:优先级越低的运算符则一定是主运算符,相同优先级的运算符一定右边的为主运算符,在这个逻辑下实现分段函数判断,返回运算符位置即可。
对表达式求值进行测试
根据框架代码产生长串表达式,并计算结果,输入到程序中。
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <assert.h>
#include <string.h>
// this should be enough
static char buf[65536] = {};
static char code_buf[65536 + 128] = {}; // a little larger than `buf`
static char *code_format =
"#include <stdio.h>\n"
"int main() { "
"unsigned result = %s; "
" printf(\"%%u\", result); "
" return 0; "
"}";
uint32_t choose(uint32_t n);
void gen_num();
void gen(char c);
void gen_rand_op();
static void gen_rand_expr() {
if(strlen(buf) > 65530)
printf("overSize\n");
switch (choose(3)) {
case 0: gen_num(); break;
case 1: gen('('); gen_rand_expr(); gen(')'); break;
default: gen_rand_expr(); gen_rand_op(); gen_rand_expr();
}
}
uint32_t choose(uint32_t n) {
return rand() % n;
}
void gen_num() {
int len = rand() % 5 + 1;
int buf_len = strlen(buf);
int i;
for (i = buf_len; i <buf_len+len; i ++) {
if(buf[buf_len-1]=='/' || i==buf_len)
//首位不能为0,且除号后面不能为0
buf[i] = rand() % 9 + 1+ '0';
else
buf[i] = rand() % 10 + '0';
}
buf[i] = 'u';
buf[i+1] = '\0';
}
void gen(char c) {
int len = strlen(buf);
buf[len] = c;
int i;
for (i = len+1; i <len+1+choose(5); i ++) {
buf[i] = ' ';
}
buf[i] = '\0';
}
void gen_rand_op() {
switch (choose(4)) {
case 0: gen('+'); break;
case 1: gen('-'); break;
case 2: gen('*'); break;
case 3: gen('/'); break;
default: assert(0);
}
}
int main(int argc, char *argv[]) {
int seed = time(0);
srand(seed);
int loop = 1;
if (argc > 1) {
sscanf(argv[1], "%d", &loop);
}
int i;
for (i = 0; i < loop; i ++) {
buf[0] = '\0';
gen_rand_expr();
sprintf(code_buf, code_format, buf);
FILE *fp = fopen("/tmp/.code.c", "w");
assert(fp != NULL);
fputs(code_buf, fp);
fclose(fp);
int ret = system("gcc /tmp/.code.c -o /tmp/.expr");
if (ret != 0) continue;
fp = popen("/tmp/.expr", "r");
assert(fp != NULL);
int result;
ret = fscanf(fp, "%d", &result);
int flag= pclose(fp);
if (flag == 0) {
//输出绿色字体
// printf("\033[32m");
// printf("Execution of /tmp/.expr succeeded.\n");
// printf("\033[0m");
} else {
//输出红色字体
// printf("\033[31m");
// printf("Execution of /tmp/.expr failed. Exit status: %d\n", result);
// printf("\033[0m");
continue;
}
//把buf中的所有u剔除掉
for(int k=0;k<strlen(buf);k++)
{
if (buf[k]=='u')
{
buf[k]=' ';
}
}
printf("%u %s\n", result, buf);
}
return 0;
}
这里遇到一个非常头大的问题:除法中除数为0的情况,如果我们要判断“/”后式子结果是否为0,就相当于又写了一次表达式求值,显然很矛盾,讲义上让我们忽略这个问题,所以我采用最笨的办法,把有错误的表达式直接掠过,只产生正确的表达式到文本中
随后在主函数中比对结果:
bool success = true;
FILE *fp;
int result;
char expression[65536];
fp = fopen("/home/chilh/ysyx-workbench/nemu/tools/gen-expr/build/input.txt", "r");
if (fp == NULL) {
printf("Failed to open input file.\n");
return 1;
}
while (fscanf(fp, "%d %[^\n]", &result, expression) == 2) {
// 在这里执行相应的计算,并输出结果
printf("Expression: %s\n", expression);
printf("Result: %u\n", result);
expr(expression, &success);
}测试中发现大量问题,一一解决后才进行下一任务
监视点
之前没用过,所以在gdb中简单使用一下,了解目的和输出格式
这边主要是对队列结构的运用,我主要使用了头插法:
WP *new_wp(char *e)
{
bool success = true;
if (free_ == NULL)
{
printf("No free watchpoint!\n");
assert(0);
}
WP *new = free_;
free_ = free_->next;
new->next = head;
strcpy(new->expr, e);
new->expr[strlen(e)] = '\0'; // 字符串结尾
new->value = expr(e, &success);
head = new;
if (success)
return new;
else
{
assert(0);
}
}
void free_wp(WP *wp)
{
if (wp == NULL)
{
printf("No such watchpoint!\n");
assert(0);
}
WP *p = head;
if (p == wp)
{
head = head->next;
wp->next = free_;
free_ = wp;
free_->expr[0] = '\0';
free_->value = 0;
return;
}
while (p->next != NULL)
{
if (p->next == wp)
{
p->next = p->next->next;
wp->next = free_;
free_ = wp;
free_->expr[0] = '\0';
free_->value = 0;
return;
}
p = p->next;
}
printf("No such watchpoint!\n");
assert(0);
}
在建立监视点时候对监视点进行表达式求值
检查监视点的值是否改变:
bool check_wp()
{ // fales表示有监视点被触发
bool success = true;
WP *p = head;
while (p != NULL)
{ // 遍历链表
word_t new_value = expr(p->expr, &success);
if (new_value != p->value)
{
printf("Watchpoint %d: %s is triggered!\n", p->NO, p->expr);
printf("Old value = 0x%08x\n", p->value);
printf("New value = 0x%08x\n", new_value);
p->value = new_value;
return false;
}
else
{
printf("No watchpoint is triggered!\n");
}
p = p->next;
}
return true;
}这里需要理解excute的代码:
把这个函数加入trace_and_difftest中并新建一个宏包裹它,实现可以在nemu/Kconfig中为监视点添加一个开关选项, 最后通过menuconfig打开这个选项, 从而激活监视点的功能. 当你不需要使用监视点时, 可以在menuconfig中关闭这个开关选项来提高NEMU的性能.
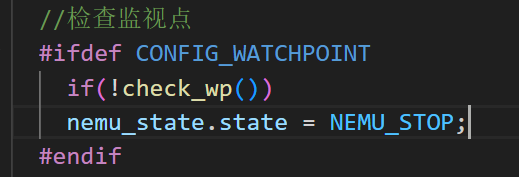
Kconfig的配置
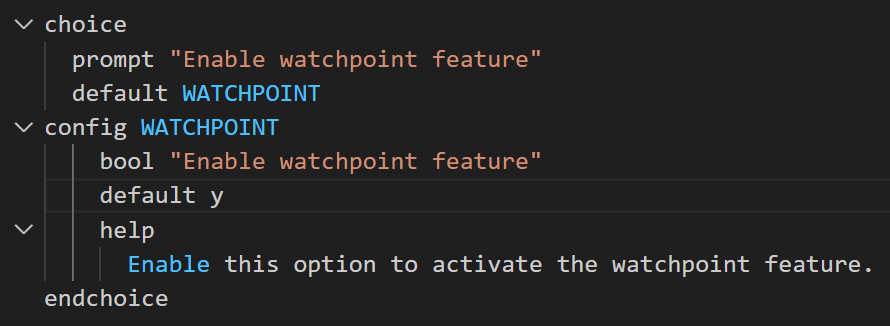
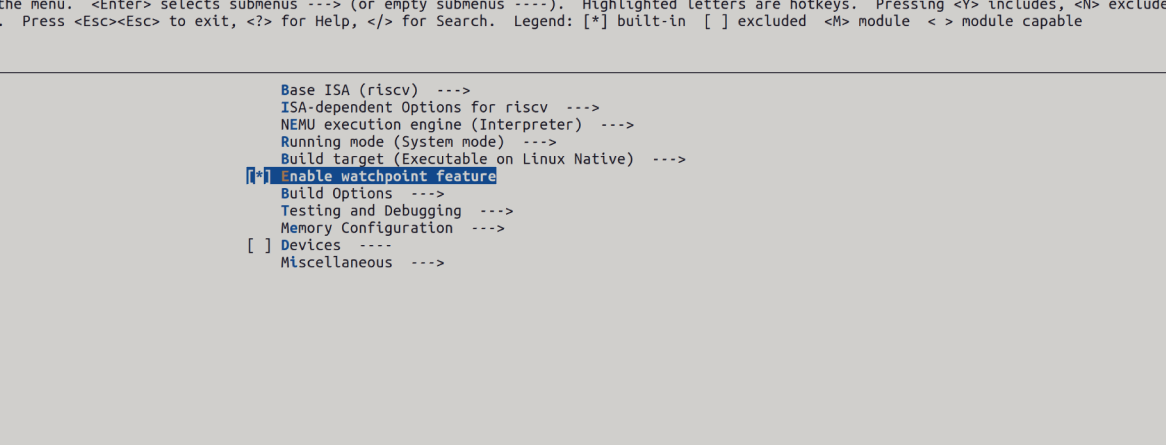
断点实现
断点的功能是让程序暂停下来, 从而方便查看程序某一时刻的状态. 事实上, 我们可以很容易地用监视点来模拟断点的功能:
w $pc == ADDR其中ADDR为设置断点的地址. 这样程序执行到ADDR的位置时就会暂停下来.
其余错误记录
错误1:由于第一位数字可能为0系统误认为是8进制数
if(i==buf_len) //首位不能为0
buf[i] = rand() % 9+1+ '0';
else
buf[i] = rand() % 10 + '0';错误2:strncpy不添加’/0‘