人工智能导论 第二章 推理
搜索及推理
题求解:在知识表达的基础上,进行机器思维,求解问题。是知识利用的基础。
求解技术:问题求解(从初始状态到目标状态)的方法和途径。与知识表达技术密切相关。
图搜索方法:基于图的知识表达。从图中相当于初始状态的出发到相当于目标状态的终止节点的路线搜索过程。
广度优先搜索,深度优先搜索….
逻辑论证法:基于谓词逻辑或其他形式逻辑方法的知识表达。
不确定性推理
非单调推理
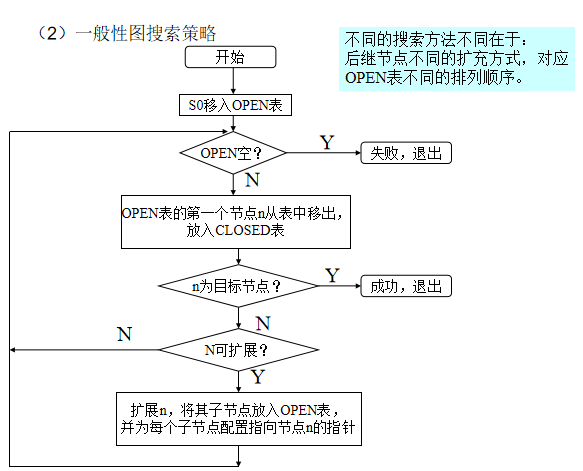
一般搜索原理
图搜索:在图中寻求从初始状态到目标状态的路径。
盲目搜索:无信息搜索,非启发性搜索。
搜索策略(盲目):
- 相关数据结构及概念:
OPEN表:用于存放刚生成的节点;
CLOSED表:用于存放将要扩展或已扩展的节点;
扩展:用定义的算子或算符对节点进行操作,生成子节点;
指针:用以记录子节点被扩展的路径,反向指向父节点;
搜索图:通过搜索所得的图;
搜索树:由搜索图中所有节点及反向指针所构成的集合。
- 相关数据结构及概念:
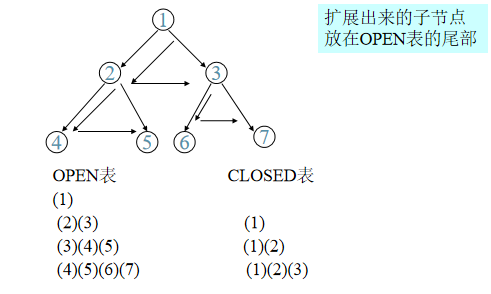
宽度优先
搜索按层进行,在对下一层节点进行搜索之前,必须搜索完本层的所有节点
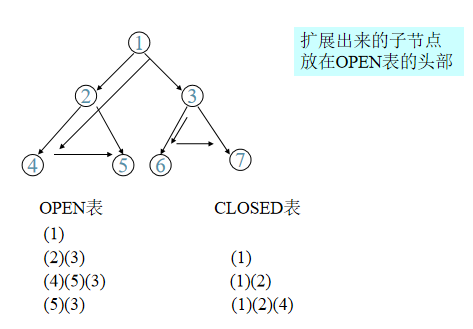
深度优先搜索
搜索按深度进行,首先扩展最新产生的节点。
有界深度优先搜索:
深度优先搜索不完备,可能陷入无限分支中,引入搜索深度界限。
启发式搜索
有信息搜索。
有序搜索:选择最有希望的节点作为待扩展节点。
通过定义某一衡量标准决定希望程度。
估价函数
估算节点希望的量度。
一般形式为:f (x) = g (x) + h (x)
f 为估价函数,f (x)表示节点x的估价函数值。
g (x)表示从初始节点到x已实际付出的代价;
h(x)是从节点x到目标节点的估计代价,利用问题本身的信息进行估价。
不同定义选最大最小
如: 宽度优先:深度小者优先;
深度优先:深度深者优先
d[n]已经付出的代价
w[n]将要付出的代价
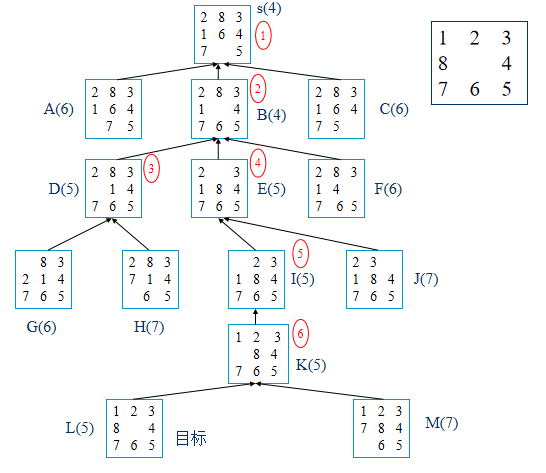
与或树
可解标识过程:由可解的子节点确定其父、祖节点可解否。(依据可解节点定义)
- 解树:由初始节点和标识初始节点可解的子节点构成。
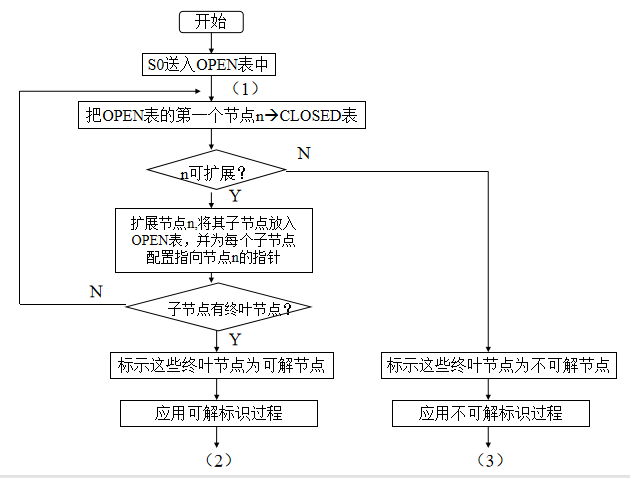
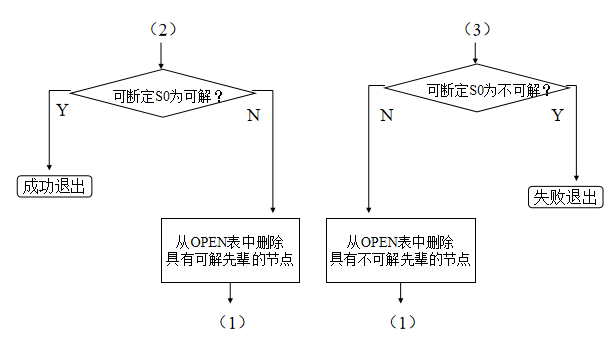
与或树的广度优先搜索
扩展节点n,将其子节点放入OPEN表的尾部,并为每个子节点配置指向节点n的指针。
与或树的深度优先搜索
扩展节点n,将其子节点放入OPEN表的首部,并为每个子节点配置指向节点n的指针。有界深度优先搜索:节点n的深度>=深度界限,则标示节点n为不可解节点。
与或树的有序搜索
依据代价决定搜索路线。

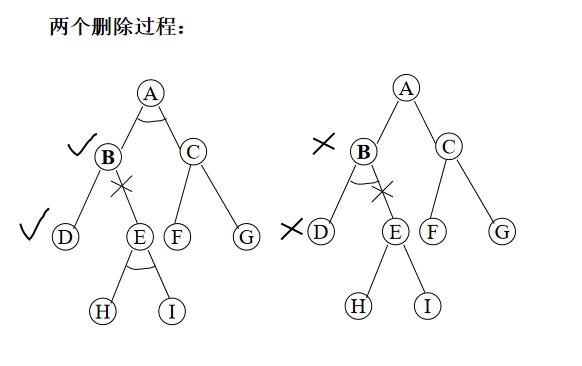
(3):与后继节点:c(x,yi)扩展代价,h(yi)后续节点代价 代价h(x)为多个后继节点中的最小值
(4): 或后继节点:求和或者取最大
红色不可解,淡蓝色可解,可解节点代价为0
2个解
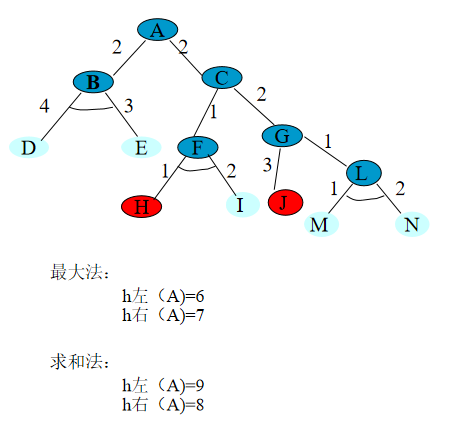
2 希望树
最优解树:代价最小的解树。
希望树T:在扩展搜索求解中,有可能成为最优解树一部分的待扩展树,当前代价最小的解树。
T包含 (1)初始节点;
(2)节点x在T中,其或后继节点中代价值最小的节点也在T中;
(3)节点x在T中,其所有与后继节点也在T中;
有序搜索过程
(1)找到希望树T;
(2)扩展其端节点n,n为可解节点,进行可解标识;不可解,则进行不可解标识;
(3)重新计算代价,回到(1)。
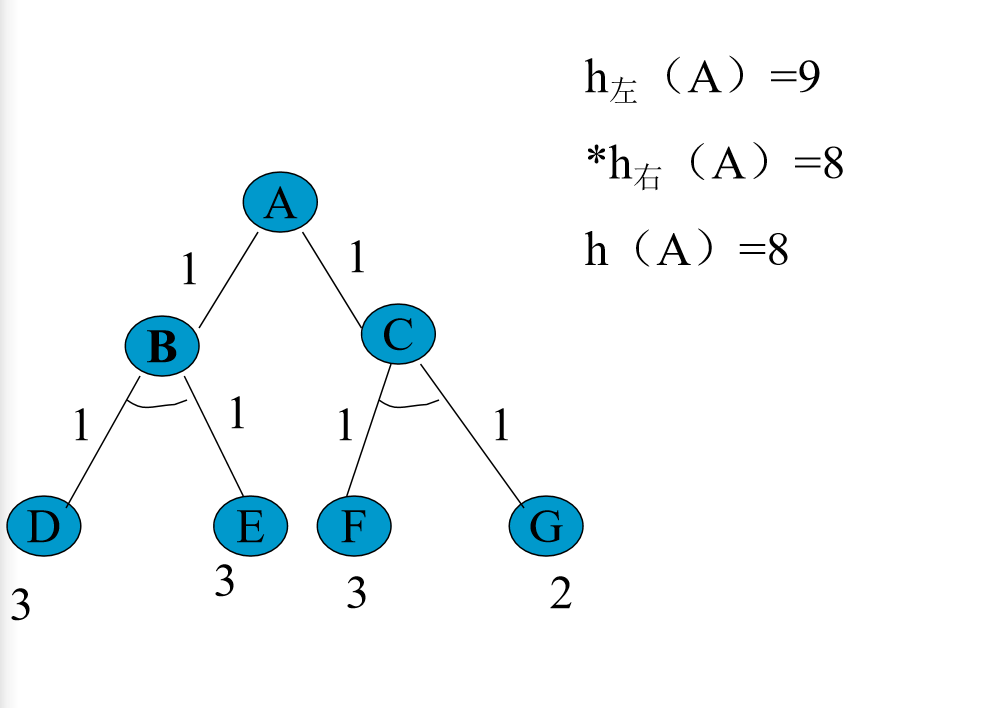
右边为希望树
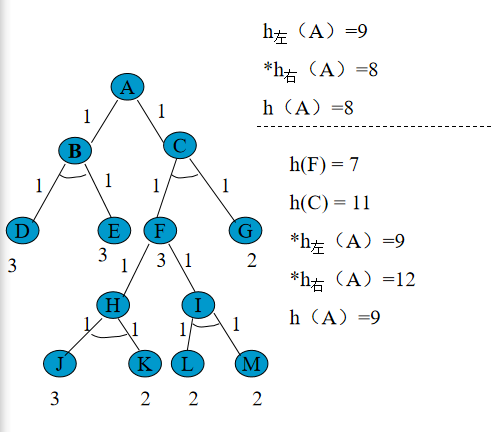
希望树变为左边

博弈树的启发式搜索
一层与节点一层或节点
博弈:
智能性的竞争活动。“二人零和,非偶然,全信息”
二人零和:得分函数之和为零,三种结局,我胜、我败、平局;
非偶然:双方皆可根据全信息进行分析,选取胜数最大的方案;
全信息:当前格局及过去,双方皆知。博弈树:描述此类过程的与或树(始终站在某一方的立场上)
(1)初始格局:初始节点;
(2)与或节点交替出现;
(3)我方扩展节点->或关系(可选择一个值大的)
敌方扩展节点->与关系(对方可能选择对我方最不利的方案)
双方轮流;
(4)使我方获胜的节点:终叶节点,可解节点;
使队方获胜的节点:不可解节点。
选出对自己最为有利的方案(树)。
3 极大极小分析法
基本思想:
预先生成一定深度博弈树;
定义估价函数,计算端节点的值(得分),静态估值,再(倒推)计算出父 节点的倒推值;
根据值选定合适的分支扩展一定的深度。
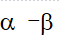 剪枝技术
剪枝技术
根据倒推值的计算方法,或中取大,与中取小,在扩展和计算过程中,能剪掉不必要的分枝,提高效率。

或节点β剪枝,与节点是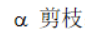
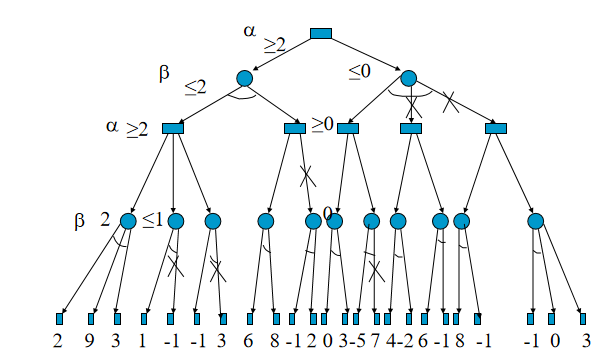
先做个说明:有画弧线的是与,取较小值,没有的是或,去最大值。
第一步:2、9、3做比较,取最小值2,I点确定为2
第二步:J点的1和I点2大小进行比较,如果1是J点的最小值,由于J的父节点是取较大值,1<2,无法升高D的值,所以J点的-1可以点可停止搜索,我们划掉该值。
第三步:I点2接着与K点的左值-1进行比较,如果-1是最小值,由于K的父节点取较大值,-1<2,无法升高D的取值,所以K点的右值可以停止搜索。
第四步:D的值可以确定为2
第五步:L点的作用值进行比较,取较小值6,D值与L值相比较,由于E去较大值,假设L就是最大值,E=6,二B点取得是D和E的较小值,2<6,E的结果值无法降低B的取值,所以E的右枝可以截掉。
第六步:B的值可以确定为2
第七步:N的左右值进行比较,取0,N点在和O点的左值-5进行比较,假设-5是最小值,0>-5,O点的取值无法升高父节点F的值,所以可以停止搜索O点的右枝。
第八步:F确定为0.
第九步:F点假设是C的最小值,它和B点的值比较,2>0,也就是说C点的取值无法升高A点的取值,所以G和H都停止搜索。
第十步:A点取2.
子句
定义:
文字:谓词逻辑中,原子谓词公式及其否定;
子句:任何文字的析取式(或);
子句集:子句的合取;
空子句:不含任何文字的子句,NIL;
化为子句集

要把否定放在原子谓词前面